dp

背包

E3-B

区间dp

C3-G

C3-J

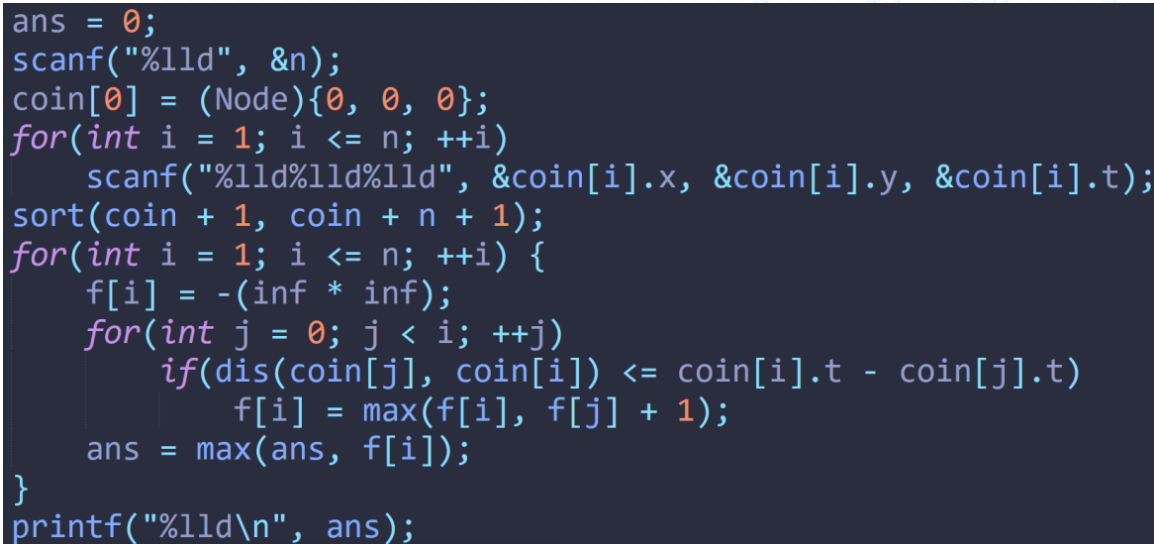
LIS

E3-H 一维金币

#include <bits/stdc++.h>  
using namespace std;  
void read (int &x) {  
    char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();  
    while (isdigit(ch)) x = x * 10 + ch - 48, ch =getchar();  
}  
const int N = 2e5 + 5, M = 10010; // 定义常量，N为金币最大数量加5，M为辅助数组大小  
int n, V, k;  
pair<int, int> p[N]; // 存储金币位置和时间-位置的数组  
int q[N], tp;// q为辅助数组，tp为q的有效长度  
void work () {  
    read (n);// 读取金币数量  
    for (int i = 1, x, t; i <= n; ++i)  
        read (x), read (t), p[i] = {x, t - x};// 位置，时间-位置  
    sort (p + 1, p + n + 1); // 按x从小到大排序  
  
    // 找到p的second的最长上升子序列  
    // t-x是指拿到这个金币之前可以有几次不用走步  
    int ans = 0; tp = 0;  // 初始化答案和辅助数组有效长度  
    for (int i = 1; i <= n; ++i) {  
        int t = p[i].second; // 获取当前金币的时间与位置差  
        if (q[tp] <= t) q[++tp] = t;  
        // 如果当前差值大于辅助数组的最后一个数（也是最大值），则添加到辅助数组  
        else if (t >= 0) { // 如果时间与位置差为非负  
            int u = upper_bound (q + 1, q + tp + 1, t) - q; // 二分查找合适的位置  
            q[u] = t; // 更新辅助数组  
        }  
    }  
    printf ("%d\n", tp);  
}  
signed main() {  
    int T; read (T);  
    while (T--) work ();  
}

其他dp

E2-G 字符串S变成回文串后的最小长度

相当于字符串S变成回文串后的最小编辑距离

• 遍历字符串的区间长度L从1到n
  • 遍历字符串的起始位置从0到n-L，字符串的终止位置为j=i+l-1
    • 如果s[i] = s[j],dp[i][j] = min(dp[i][j],dp[i+1][j-1]);
    • 否则dp[i][j] = min(dp[i][j],dp[i+1][j],dp[i][j-1])

#include <bits/stdc++.h>  
#define get(l, r) ((l) <= (r) ? (dp[l][r]) : (0))  
  
using namespace std;  
  
const int inf = 1e9;  
  
int main() {  
    ios::sync_with_stdio(false);  
    cin.tie(0);  
    int tt;  
    cin >> tt;  
    while (tt--) {  
        int n;  
        cin >> n;  
        string s;  
        cin >> s;  
        vector<vector<int>> dp(n, vector<int>(n, inf));  
        for (int l = 1; l <= n; l++) {  
            for (int i = 0; i < n; i++) {  
                int j = i + l - 1;  
                if (j >= n) {  
                    break;  
                }  
                if (s[i] == s[j]) {  
                    dp[i][j] = min(dp[i][j], get(i + 1, j - 1));  
                } else {  
                    dp[i][j] = min(dp[i][j], min(get(i + 1, j), get(i, j - 1)) + 1);  
                }  
            }  
        }  
        cout << dp[0][n - 1] + n << '\n';  
    }  
    return 0;  
}

E2-J 任务达人莫卡

• one和two变量分别用于存储所有城市中的最大和次大收益。
• 遍历每天， f[c[i]] += a[c[i]]
  • 如果那天的任务城市在那天之前的价值 tmp==one，则更新那天的任务城市的价值为 max (f[c[i]], two + b[c[i]]) （因为从前一次去那个城市之后不去其他城市的价值为 f[c[i]]，去了其他城市之后得到的最大价值为 two ）
  • 如果那天的任务城市在那天之前的价值 tmp!=one，则更新那天的任务城市的价值为 max (f[c[i]], one + b[c[i]]) （因为从前一次去那个城市之后不去其他城市的价值为 f[c[i]]，去了其他城市之后得到的最大价值为 one ）
  • 然后更新 one 和 two

E2-K 二维金币

贪心

C4-D 切钢条

#include <bits/stdc++.h>  
using namespace std;  
priority_queue <long long,vector<long long>,greater<long long>> len;  
  
int main(){  
    int n;  
    long long ans = 0;  
    scanf("%d", &n);  
    for(int i=0; i<n; i++){  
        long long l;  
        scanf("%lld", &l);  
        len.push(l);  
    }  
  
    for(int i=0; i<n-1; i++){  
        long long tempAns = 0;  
        long long temp1 = len.top();  
        len.pop();  
        tempAns += temp1;  
        temp1 = len.top();  
        len.pop();  
        tempAns += temp1;  
        len.push(tempAns);  
        ans += tempAns*2;  
    }  
    printf("%lld", ans);  
}

相当于洛谷p1090 合并果子

图论

最短路

E4-D 2024-CYCLES

找带权有向图上环的权值的最小值（定义环的权值为环上所有边的边权平均值）。
转化为二分查找环的权值，最初min = 0, max = 1e7，二分查找50次。如果有环的权值为v的环，把所有的边的权值-v后，有负环，因此每次查找都dfs看所有的点是否有负环。即下面代码中的 dfs 函数

#include <cstdio>

using namespace std;

const int N = 1e3 + 5; // 定义节点数的最大值

int n, m; // n为节点数，m为边数
int h[N], to[N], nx[N], et; // 邻接表存储图，h为头节点数组，to为终点数组，nx为下一个边数组，et为边的计数
double wt[N], dis[N]; // wt为边权数组，dis为距离数组
bool vis[N]; // vis为访问标记数组

// 添加边的函数
void ae(int u, int v, double w) {
    et++; // 边计数增加
    to[et] = v; // 设置边的终点
    wt[et] = w; // 设置边的权重
    nx[et] = h[u]; // 设置下一个边
    h[u] = et; // 更新头节点
}

// 深度优先搜索，用于检测负环
bool dfs(int u, double v) {
    if (vis[u]) // 如果当前节点已访问，说明存在环
        return 1;
    vis[u] = 1; // 标记当前节点为已访问
    for (int i = h[u]; i; i = nx[i]) // 遍历所有邻接边
        if (dis[u] + wt[i] - v < dis[to[i]]) { // 如果找到更短的路径
            dis[to[i]] = dis[u] + wt[i] - v; // 更新距离
            if (dfs(to[i], v)) { // 递归检测环
                vis[u] = 0; // 回溯时取消标记
                return 1; // 发现环
            }
        }
    vis[u] = 0; // 回溯时取消标记
    return 0; // 未发现环
}

// 检查是否存在负环
bool check(double v) {
    for (int i = 1; i <= n; i++)
        dis[i] = 0; // 初始化距离数组
    for (int i = 1; i <= n; i++)
        if (dfs(i, v)) // 有负环
            return 1; // 返回真
    return 0; // 未发现环，返回假
}

// 解决问题的函数
void solve() {
    scanf("%d%d", &n, &m); // 读取节点数和边数
    for (int i = 1; i <= n; i++)
        h[i] = 0; // 初始化头节点数组
    et = 0; // 初始化边计数
    for (int i = 1; i <= m; i++) {
        int u, v;
        double w;
        scanf("%d%d%lf", &u, &v, &w); // 读取边的信息
        ae(u, v, w); // 添加边
    }
    double l = 0, r = 1e7; // 二分查找的左右边界
    for (int i = 1; i <= 50; i++) { // 进行50次二分查找
        double mid = (l + r) / 2; // 计算中点
        if (check(mid)) // 有负环，说明存在比mid小的环
            r = mid; // 缩小右边界
        else
            l = mid; // 缩小左边界
    }
    if (l > 5e6) // 如果左边界大于5e6，说明没有环
        l = 0; // 设置答案为0
    printf("%.4lf\n", l); // 输出答案，保留4位小数
}

int main() {
    int T;
    scanf("%d", &T); // 读取数据组数
    while (T--)
        solve(); // 对每组数据求解
    return 0;
}

E5-H 重生之被困在大富翁地图

dijsktra

#include<bits/stdc++.h>  
using namespace std;  
const int N=1e5+5; // 定义节点数的最大值  
// 定义节点结构体，用于优先队列  
struct Node{  
    int p,dis;  
    // 重载小于号，实则重载的是大于号，因为默认是大根堆  
    bool operator<(const Node &b)const{  
        return dis>b.dis;  
    }  
};  
int adj[N],to[N<<1],nxt[N<<1],tot; // 邻接表存储图，to存储目标节点，nxt存储下一个边，tot存储边的总数  
int dis[N]; // 存储从起点到每个节点的最小能量消耗  
priority_queue<Node>q; // 优先队列，用于Dijkstra算法  
void addedge(int f,int t);  
void dij(int sp,int pdis);  
  
int main(){  
    int T;  
    scanf("%d",&T); // 读取数据组数  
    while(T--) { // 对每组数据进行处理  
        int n,t,a0=0;  
        scanf("%d%d",&n,&t);t++; // 读取节点数和目标节点，节点编号从1开始  
        memset(adj,0,sizeof adj);tot=0; // 初始化邻接表  
        for(int i=0;i<n;i++){  
            int a;scanf("%d",&a);  
            addedge(i,(i+1)%n),addedge(i,(i+a)%n); // 添加两条边，一条是走到下一个格子，另一条是走a个格子  
            // 如格子0有a0=2，所以它有边连向a1和a2。我选择操作1+操作2，即走3个格子，相当于走到a2在走到a3  
            // 也就是说“走到下一个格子”的这条边是供从上一个格子走到这里时想要做的操作1，只不过我们交换了操作1和操作2的执行顺序  
            // 也因此，下面!i即i == 0时，由于起点前没有其他点了，所以起点相当于只能做操作2，所以a0 = a，第一步走了a  
            // （实际上起点是可以进行操作1的，只不过我们是在走了a步后，即操作2结束后再进行的操作1）  
            if(!i) a0=a; // 记录起点的a值  
        }  
        dij(a0+1,1); // 从起点开始运行Dijkstra算法，起点能量消耗为1  
        printf("%d\n",dis[t]); // 输出到达目标节点的最小能量消耗  
    }  
    return 0;  
}  
  
// 添加边的函数，由于地图是环形的，所以需要对节点编号进行模运算  
void addedge(int f,int t){  
    f++,t++; // 节点编号从1开始，所以需要加1  
    to[++tot]=t,nxt[tot]=adj[f],adj[f]=tot; // 添加边  
}  
  
// Dijkstra算法实现  
void dij(int sp,int pdis){  
    memset(dis,0x3f,sizeof(dis)); // 初始化距离数组为无穷大  
    dis[sp]=pdis; // 起点的能量消耗为0  
    q.push({sp,pdis}); // 将起点加入优先队列  
    while(!q.empty()){ // 主循环  
        Node x=q.top();q.pop(); // 取出当前能量消耗最小的节点  
        if(x.dis!=dis[x.p]) continue; // 如果取出的能量消耗不是最新的，则跳过  
        for(int i=adj[x.p];i;i=nxt[i]){ // 遍历所有邻接节点  
            if(dis[to[i]]>x.dis+1){ // 如果找到更小的能量消耗，则更新  
                dis[to[i]]=x.dis+1;  
                q.push({to[i],x.dis+1}); // 将新能量消耗的节点加入优先队列  
            }  
        }  
    }  
}

BFS求无权图最短路：E2-F Maze No.9

真看不下去了