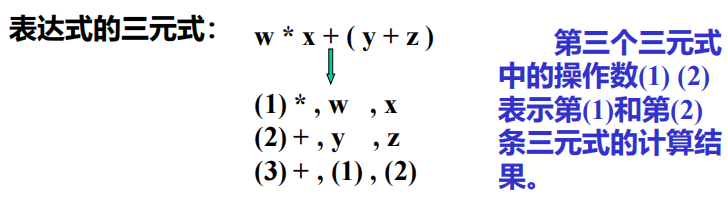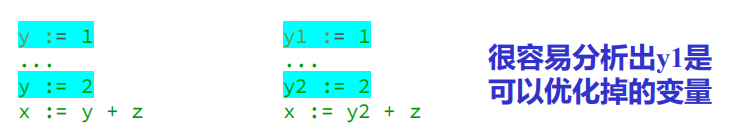1 波兰表示(后缀遍历)
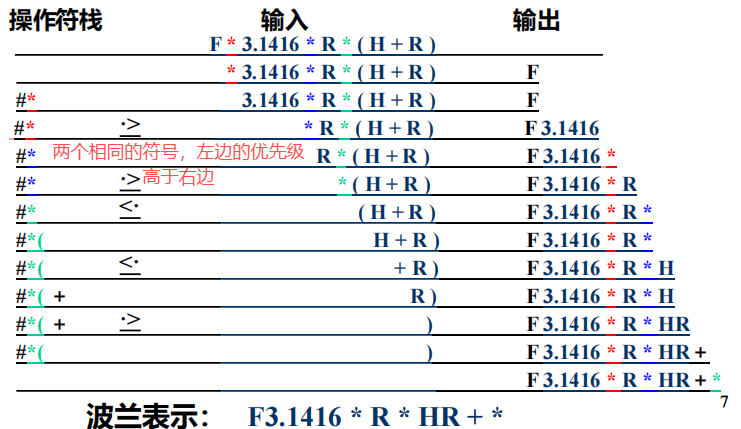
算术表达式: F 3.1416 R ( H + R )
转换成波兰表示: F 3.1416 R H R +
- 优势
- 在不使用括号的情况下可以无二义地说明算术表达式。
- 波兰表示法更容易转换成机器的汇编语言或机器语言。
操作数出现在紧靠操作符的左边,而操作符在波兰表示中的顺序即为进行计算的顺序。 - 波兰表示不仅能用来作为算术表达式的中间代码形式,而且也能作为其它语言结构的中间代码形式。
1 转换算法
当读到操作数时,就立即输出该操作数;当遇到操作符时,则要与栈顶操作符比较优先级,若栈顶操作符优先级高于栈外,则输出该栈顶操作符;反之,则栈外操作符入栈。
对于赋值语句,则需规定赋值符号的优先级低于其它操作符,所以:
赋值语句的波兰表示 A := F 3.1416 R ( H + R )
A F 3.1416 R H R + :=
例子
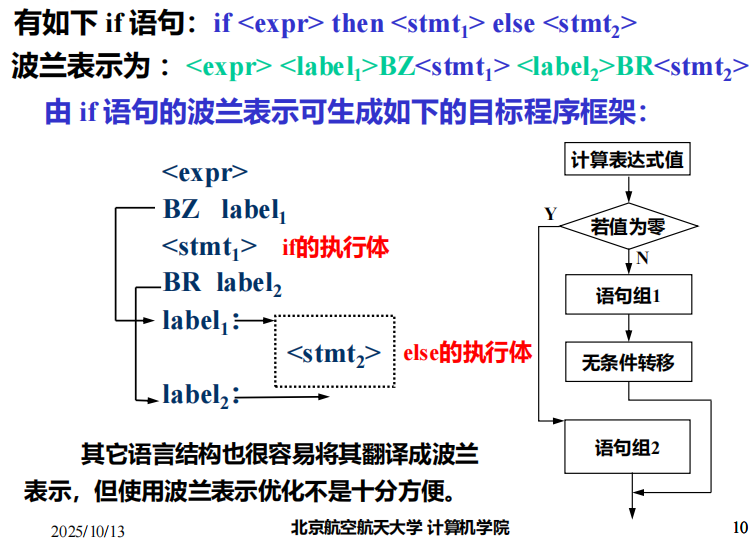
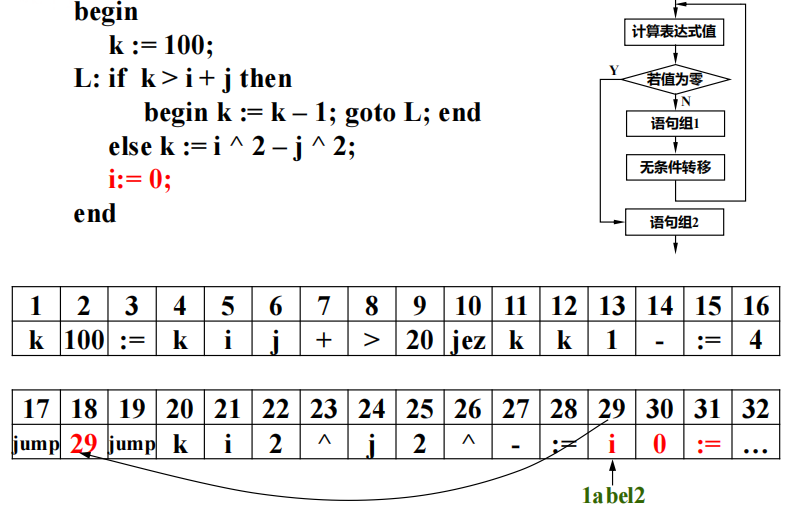
2 if 语句的波兰表示
here 录屏
例子
2 N-元表示
2.1 三元式
- 在该表示中,每条指令由 n 个域所组成,通常第一个域表示操作符,其余为操作数。
- 常用的 n 元表示是: 三元式 四元式
三元式:操作符、左操作数、右操作数
2.2 三元式 pro——间接三元式
- 使用三元式也不便于代码优化,因为优化要删除一些三元式,或对某些三元式的位置要进行变更,由于三元式的结果(表示为编号),可以是某个三元式的操作数,随着三元式位置的变更也将作相应的修改,很费事!
- 间接三元式:为了便于在三元式上作优化处理,可使用间接三元式。
例子
进行如下代码优化
后续的三元式的编号也会一起发生变化,可能影响到后续三元式的计算
- 间接三元式:三元式的执行次序用(操作)另一张表表示,这样在优化时(三元式位置的变更实际是执行顺序的变化),三元式可以不变,而仅仅改变其执行顺序表。
2.3 四元式
- 四元式表示:操作符 操作数1 操作数2 结果
- 结果:通常是编译时分配的临时变量,可由编译程序分配一个寄存器或主存单元。
例子
优化:T1*T2 再存到 T1 里面,T3(T1)-E 再存到 T2 里面
3 抽象机代码
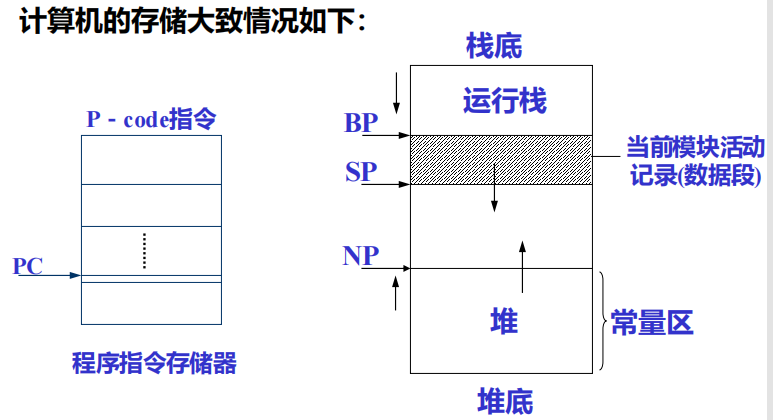
既然是“抽象机”,就是表示它并不是实际的物理目标机器而通常是虚拟的一台“堆栈计算机”。该堆栈式计算机主要由若干寄存器、一个保存程序指令的储存器和一个堆栈式数据及操作存储组成。
寄存器有:
- PC —— 程序计数器。
- NP —— New指针,指向“堆”的顶部。“堆”用来存放由NEW生成的动态数据。
- SP —— 运行栈指针,存放所有可按源程序的数据声明直接寻址的数据。
- BP ——基地址指针,即指向当前活动记录的起始位置指针。
- 其他(如MP—栈标志指针,EP—极限栈指针等)
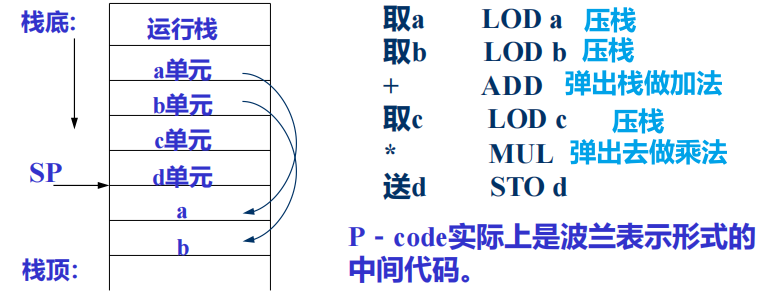
- 运行P– code的抽象机没有专门的运算器或累加器,所有的运算(操作)都在运行栈的栈顶进行,如要进行d := ( a + b ) * c的运算,生成P– code序列为:
- 编译程序生成P – code指令程序后,我们可以用一个解释执行程序(interpreter)来解释执行P – code ,当然也可以把P – code再变成某一机器的目标代码。显然,生成抽象机P – code的编译程序是很容易移植的。
4 其他形式的中间代码
4.1 二叉数表示
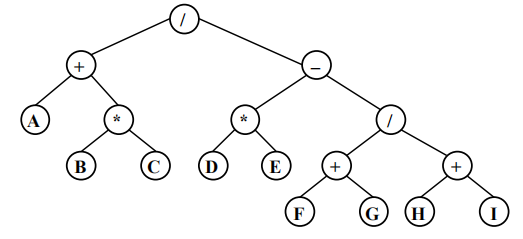
操作数出现在叶节点上,操作符出现在中间结点。
例子
例如:(A+B*C)/(D*E-(F+G)/(H+I))
4.2 图表示
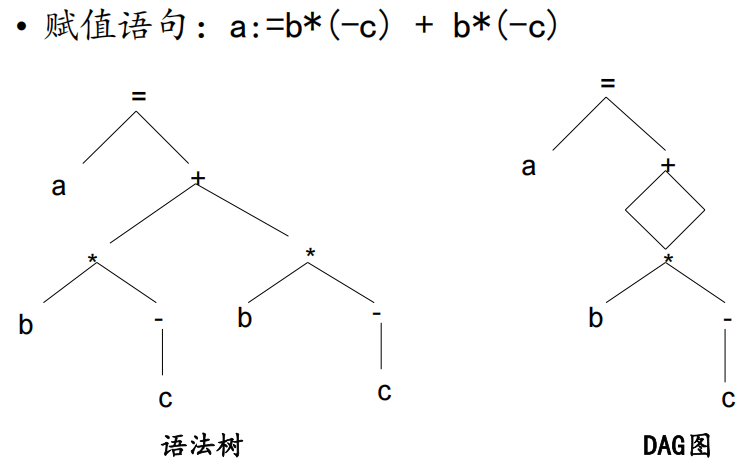
DAG图(Directed Acyclic Graphs 有向无环图)––语法树的一种归约表达方式
- 图的叶节点由变量名或常量所标记。对于那些在基本块内先引用再赋值的变量,可以采用变量名加下标0的方式命名其初值。
- 图的中间节点由中间代码的操作符所标记,代表着基本块中一条或多条中间代码。
- 基本块中变量的最终计算结果,都对应着图中的一个节点;具有初值的变量,其初值和最终值可以分别对应不同的节点。
例子
4.3 三地址码
-
三地址码(英语:Three address code,经常被缩写为TAC 或 3AC)
-
中间语言,编译器使用它来改进代码转换效率。
-
每个三地址码指令都可以被分解为一个四元组:(运算符,操作数1,操作数2,结果)。
-
因为每个陈述都包含了三个变量,所以它被称为三地址码。
-
适合目标代码生成和优化的一种表达形式
-
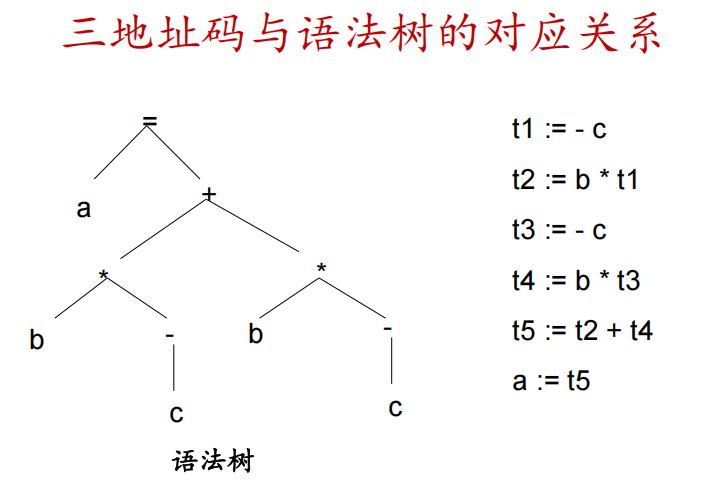
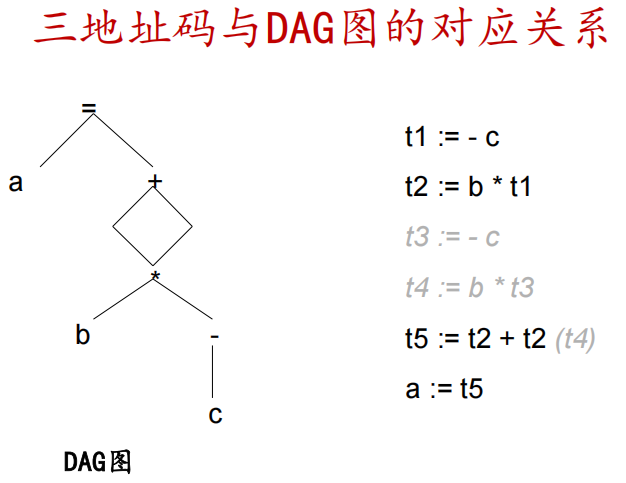
三地址码是语法树或者DAG图的线性表示
-
树的中间结点由临时变量表示
例子
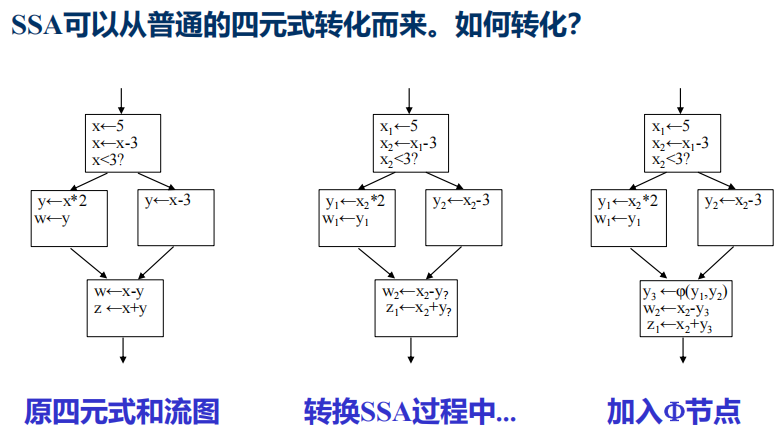
4.4 一种特殊的四元式表达方式 :SSA
- Single Static Assignment form (SSA form) 静态单一赋值
形式的 IR 主要特征是每个变量只赋值一次。 - SSA的优点
- 可以简化很多优化的过程;
- 可以获得更好的优化结果。
例子