15 动态规划

  • 动态规划方法通常用来求解最优化问题（optimization problem）。
  • 动态规划算法设计步骤：
    • 刻画一个最优解的结构特征；
    • 递归定义最优解的值；
    • 计算最优解的值，通常采用自底向上的方法；
    • 利用计算出的信息构造一个最优解。
  • 最优子结构性质：问题的最优解由相关子问题的最优解组合而成，而这些问题可以独立求解。

15.1 钢条切割

15.1.1 题目介绍

给定一段长度为 英寸的钢条和一个价格表 ，求切割钢条方案，使得销售收益 最大。注意，如果长度为 英寸的钢条的价格 足够大，最优解可能就是完全不需要切割。

  • Pasted image 20241005225927.pngPasted image 20241005225950.png

15.1.2 法1：自顶向下递归实现

  • 思路：我们将钢条从左边切割下长度为 的一段，只对右边剩下的长度为 的一段继续进行切割（递归求解），对左边的一段则不在进行切割。即问题分解的方式为：将长度为 的钢条分解为左边开始一段，以及剩余部分继续分解的结果。这样，不做任何切割的方案就可以描述为：第一段的长度为 ，收益为 ，剩余部分长度为 ，对应的收益为 。于是我们可以得到公式：。
  • 伪代码
CUT_ROD(p, n)

if n == 0
	 return 0
q = -∞
for i = 1 to n
	 q = max(q, p[i]+CUT_ROD(p, n-1))
return q
  • 复杂度：

15.1.3 !法2：带备忘的自顶向下法(top-down with memoization)

  • 思路
    此方法仍按自然的递归形式编写过程，但过程会保存每个子问题的解（通常保存在一个数组或散列表中）。当需要一个子问题的解时，过程首先检查是否已经保存过此解。如果是，则直接返回保存的值，从而节省了计算时间；否则，按通常方式计算这个子问题。我们称这个递归过程是带备忘的(memoized)，因为它“记住”了之前已经计算出的结果，
  • 伪代码
MEMOIZED_CUT_ROD(p, n)
	 let r[0..n] be a new array
	 for i = 0 to n
		 r[i] = -∞
	 return MEMOIZED_CUT_ROD_AUX(p, n, r)

MEMOIZED_CUT_ROD_AUX(p, n, r)
	 if r[n] >= 0
		 return r[n]
	 if n == 0
		 q = 0
	 else
		 q = -∞
		 for i = 1 to n
			 q = max(q, p[i] + MEMOIZED_CUT_ROD_AUX(p, n-i, r))
	 r[n] = q
	 return q
  • c语言实现
int max(int a, int b){  
   if(a > b){  
       return a;  
   }else{  
       return b;  
   }  
}  
 
int MEMOIZED_CUT_ROD_AUX(int* p, int n, int* r){  
   int q;  
   if(r[n] >= 0){  
       return r[n];  
   }  
   if(n == 0){  
       q = 0;  
   }else{  
       q = -1;  
       for(int i=1; i<=n; i++){  
           q = max(q, p[i]+MEMOIZED_CUT_ROD_AUX(p, n-i, r));  
       }  
   }  
   r[n] = q;  
   return q;  
}  
 
int MEMOIZED_CUT_ROD(int* p, int n){  
   int r[MAX];  
   for(int i=0; i<=n; i++){  
       r[i] = -1;  
   }  
   return MEMOIZED_CUT_ROD_AUX(p, n, r);  
}
  • 复杂度：

15.1.4 !法3：自底向上法(bottom-up method)

  • 思路
    这种方法一般需要恰当定义子问题“规模的概念”，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因而我们可以将子问题按规模排序，按由小至大的顺序进行求解。当求解某个子问题时，它所依赖的那些更小的子问题都已求解完毕，结果已经保存。每个子问题只需求解一次，当我们求解它（也是第一次遇到它）时，它的所有前提子问题都已求解完成。
  • 伪代码
BOTTOM_UP_CUT_ROD(p, n)
	 let r[0..n] be a new array
	 r[0] = 0
	 for j = 1 to n
		 q = -∞
		 for i = 1 to j
			 q = max(q, p[i] + r[j-i])
		 r[j] = q
	 return r[n]
  • c语言实现
int max(int a, int b){  
   if(a > b){  
       return a;  
   }else{  
       return b;  
   }  
}  
 
int BOTTOM_UP_CUT_ROD(int *p, int n){  
   int r[MAX];  
   r[0] = 0;  
   for(int j=1; j<=n; j++){  
       int q = -1;  
       for(int i=1; i<=j; i++){  
           q = max(q, p[i] + r[j-i]);  
       }  
       r[j] = q;  
   }  
   return r[n];  
}
  • 复杂度：

15.1.5 !给出最大收益及最优切割方案

  • 思路：
    • 前文给出的钢条切割问题的动态规划算法返回最优解的收益值，但并未返回解本身（一个长度列表，给出切割后每段钢条的长度）。我们可以扩展动态规划算法，使之对每个子问题不仅保存最优收益值，还保存对应的切割方案。利用这些信息，我们就能输出最优解。下面的 EXTENDED_BOTTOM_UP_CUT_ROD 对长度为 的钢条不仅计算最大收益值 ，还保存最优解对应的第一段钢条的切割长度 。
    • PRINT_CUT_ROD_SOLUTION 接受两个参数：价格表 和钢条长度 ，然后调用 EXTENDED-BOTTOM-UPCUT-ROD 来计算切割下来的每段钢条的长度 ，最后输出长度为 的钢条的完整的最优切割方案。
  • 伪代码
EXTENDED_BOTTOM_UP_CUT_ROD(p, n)
	let r[0..n] ans s[0..n] be new arrays
	r[0] = 0
	for j = 1 to n
		q = -∞
		for i = 1 to j
			if q < p[i]+r[j-i]
				q = p[i]+r[j-i]
				s[j] = i
		r[j] = q
	return r ans s

PRINT_CUT_ROD_SOLUTION(p, n)
	(r, s) = EXTENDED_BOTTOM_UP_CUT_ROD(p, n)
	while n > 0
		print s[n]
		n = n-s[n]
  • c语言实现
int s[MAX], r[MAX];  
void EXTENDED_BOTTOM_UP_CUT_ROD(int *p, int n){  
    r[0] = 0;  
    for(int j=1; j<=n; j++){  
        int q = -1;  
        for(int i=1; i<=j; i++){  
            if(q < p[i]+r[j-i]){  
                q = p[i]+r[j-i];  
                s[j] = i;  
            }  
        }  
        r[j] = q;  
    }  
}  
  
void PRINT_CUT_ROD_SOLUTION(int *p,int n){  
    EXTENDED_BOTTOM_UP_CUT_ROD(p, n);  
    while(n > 0){  
        printf("%d ", s[n]);  
        n -= s[n];  
    }  
}

15.1.6 子问题图

Pasted image 20241005235554.png

15.2 矩阵链乘法

15.2.1 题目介绍

  • 我们称有如下性质的矩阵乘积链的积是完全括号化的（fully parenthesized）：它是单一矩阵，或者是两个完全括号化的矩阵乘积链的积，且已外加括号。
    例如，如果矩阵链为，则共有5种完全括号化的矩阵乘积链：
  • 矩阵链乘法问题（matrix-chain multiplication problem）可描述如下：给定n个矩阵的链，矩阵是规模为 ，求完全括号化方案，使得计算乘积 所需标量乘法次数最少。

15.2.2 思路&伪代码

步骤1：最优括号化方案的结构特征

  • 假设 的最优括号化方案的分割点在 和 之间，那么对子链 和 进行括号化的方法，就是它自身的最优括号化方案
  • 也就是说，为了构造一个矩阵链乘法问题实例的最优解，我们可以将问题划分为两个子问题（ 和 的最优括号化问题），求出子问题实例的最优解，然后将子问题的最优解组合起来。

步骤2：一个递归求解方案

对矩阵链乘法问题，我们可以将对所有 确定 的最小代价括号化方案作为子问题。令 表示计算矩阵 所需标量乘法次数的最小值，那么，原问题的最优解——计算 所需的最低代价就是 。因此， 最小代价括号化方案的递归求解公式变为：

如果如果

的值给出了子问题最优解的代价，但它并未提供足够的信息来构造最优解。为此，我们用 保存 最优括号化方案的分割点位置 ，即使得 成立的 值。

步骤3：计算最优代价

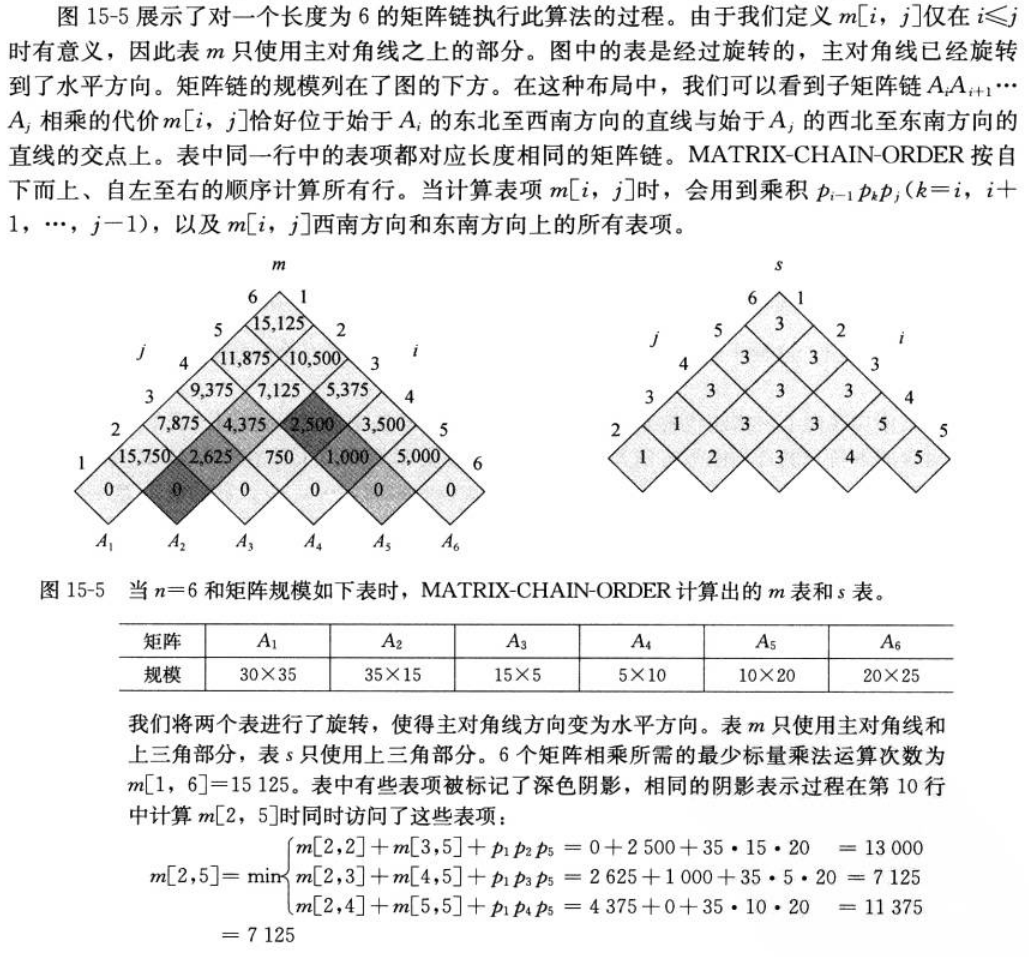
  • 伪代码
MATRIX_CHAIN_ORDER(p)
	n = p.length-1
	let m[1..n,1..n] and s[1..n,1..n] be new tables
	for i = 1 to n
		m[i,i] = 0
	for l = 2 to n    // l is the chain length
		for i = 1 to n-l+1
			j = i+l-1
			m[i,j] = ∞
			for k = i to j-1
				q = m[i,k] + m[k+1,j] + p[i-1]*p[k]*p[j]
				if q < m[i,j]
					m[i.j] = q
					s[i,j] = k
	return m and s

Pasted image 20241008111331.png

  • 例
    Pasted image 20241008111402.png

步骤4：构造最优解

每个表项 记录了一个 值，指出 的最优括号化方案的分割点应在 和 之间。因此，我们知道 的最优计算方案中最后一次矩阵乘法运算应该是 。我们可以用相同的方法递归地求出更早的矩阵乘法的具体计算过程。下面给出的递归过程可以输出 的最优括号化方案，其输入为MATRIX_CHAIN_ORDER得到的表s及下标i和j。调用PRINT_OPTIMAL_PARENS(s,1,n)即可输出 的最优括号化方案。

PRINT_OPTIMAL_PARENS(s,i,j)
	if i == j
		print"A"
	else
		print"("
		PRINT_OPTIMAL_PARENS(s,i,s[i,j])
		PRINT_OPTIMAL_PARENS(s,s[i,j]+1,j)
		print")"

15.2.3 !c语言实现

/*  
 * p: 表示矩阵的规模，矩阵 A_i 的规模用 p_i-1 * p_i 表示  
 * m: 计算矩阵A_i..j所需标量乘法次数的最小值  
 * s: s[i,j]表示A_i A_i+1 ... A_j最优括号化方案的分割点位置k  
 */
#define MAX 100  
long long p[MAX],m[MAX][MAX],s[MAX][MAX];  
void MATRIX_CHAIN_ORDER(int n){  
    for(int i=1; i<=n; i++){  
        m[i][i] = 0;  
    }  
    for(int l=2; l<=n; l++){    // l is the chain length  
        for(int i=1; i<=n-l+1; i++){  
            int j = i+l-1;  
            m[i][j] = 9223372036854775807;  // long long 最大值  
            for(int k=i; k<=j-1; k++){  
                long long q = m[i][k]+m[k+1][j] + p[i-1]*p[k]*p[j];  
                if(q < m[i][j]){  
                    m[i][j] = q;  
                    s[i][j] = k;  
                }  
            }  
        }  
    }  
}  
void PRINT_OPTIMAL_PARENS(long long i, long long j){  
    if(i == j){  
        printf("A");  
    }else{  
        printf("(");  
        PRINT_OPTIMAL_PARENS(i, s[i][j]);  
        PRINT_OPTIMAL_PARENS(s[i][j]+1, j);  
        printf(")");  
    }  
}  
int main() {  
    int n;  
    scanf("%d", &n);  
    for(int i=0; i<=n; i++){  
        scanf("%lld", &p[i]);  
    }  
    MATRIX_CHAIN_ORDER(n);  
    PRINT_OPTIMAL_PARENS(1,n);  
    return 0;  
}

15.4 最长公共子序列

15.4.1 题目介绍

  • 子序列：给定一个序列 ，另一个序列 满足如下条件时成为 的子序列（subsequence），即存在一个严格递增的 的下表序列 ，对所有 ，满足 。
    例如， 是 的子序列，对应的下标序列为 。
  • 公共子序列：给定两个序列 和 ，如果 Z 既是 X 的子序列，也是 Y 的子序列，我们称它是 X 和 Y 的公共子序列（common subsequence）。
    例如，如果 ，那么序列 就是 和 的公共子序列。但它不是 和 的最长公共子序列（LCS），因为它长度为3，而 也是 和 的公共子序列，其长度为4。 是 和 的最长公共子序列， 也是，因为 X 和 Y 不存在长度大于等于5的公共子序列。
  • 最长公共子序列问题（longest-common-subsequence problem）：给定两个序列 和 ，求 和 长度最长的公共子序列。

15.4.2 思路&伪代码

步骤1：刻画最长公共子序列的特征

令 和 为两个序列， 为 和 的任意 。

  • 如果 ，则 且 是 和 的一个 。
  • 如果 ，则 意味着 是 和 的一个 。
  • 如果 ，则 且 是 和 的一个 。

步骤2：递归式

定义 表示 和 的 的长度，得到如下公式：

若或若且若且

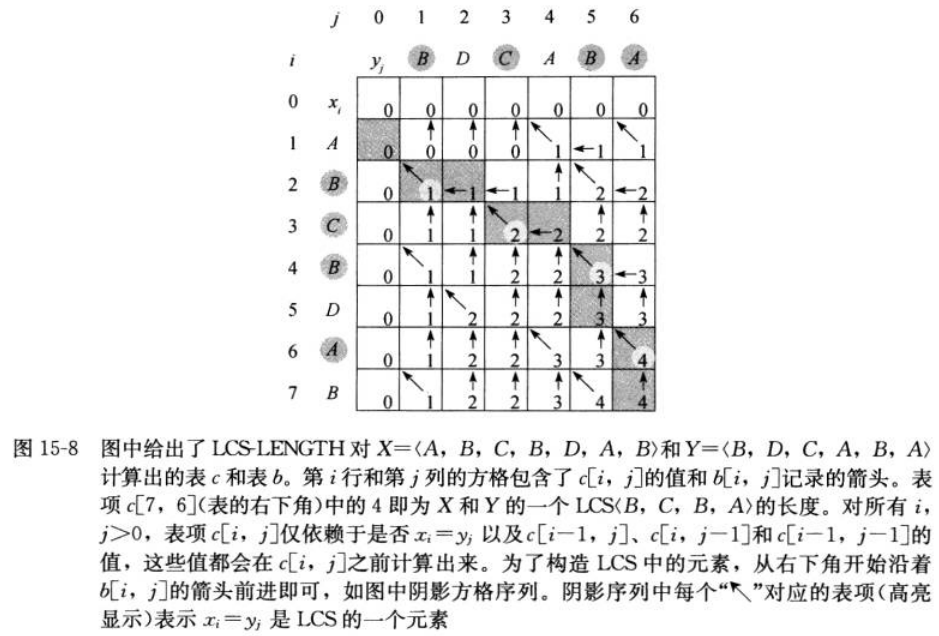
步骤3：计算LCS的长度（自底向上）

过程 LCS_LENGTH 接受两个序列 和 为输入。它将 的值保存在表 中，并按行主次序（row-major order）计算表项（即首先由左至右边计算c的第一行，然后计算第二行，依此类推）。过程还维护一个表 ，帮助构造最优解。指向的表项对应计算 时所选择的子问题最优解。过程返回表b和表c， 保存了 和 的 的长度。
Pasted image 20241006211217.png
Pasted image 20241006211250.png

步骤4：构造LCS

Pasted image 20241006211558.png

特别地，我们可以去掉表b，因为每个 项只依赖于表c中的其他三项：、 和 。给定 的值，我们可以在 时间内判断出在计算 时使用了这三项中的哪一项。

如果只需要计算 的长度，只需要保存表c中的两行（当前正在计算的一行和前一行）

15.4.3 !c语言实现

复杂度：

#include <stdio.h>  
#include <string.h>  
#define MAX 100  
  
int c[MAX][MAX]={};  
void LCS_LENGTH(char *x, char *y){  
    int xLen = strlen(x), yLen = strlen(y);  
    for(int i=1; i<xLen; i++){  
        if(y[0] == x[i] || c[i-1][0] == 1){  
            c[i][0] = 1;  
        }  
    }  
    for(int i=1; i<yLen; i++){  
        if(x[0] == y[i] || c[0][i-1] == 1){  
            c[0][i] = 1;  
        }  
    }  
    for(int i=1; i<xLen; i++){  
        for(int j=1; j<yLen; j++){  
            if(x[i] == y[j]){  
                c[i][j] = c[i-1][j-1] + 1;  
            }else if(c[i-1][j] >= c[i][j-1]){  
                c[i][j] = c[i-1][j];  
            }else{  
                c[i][j] = c[i][j-1];  
            }  
        }  
    }  
}  
  
void PRINT_LCS(char *x, char *y, int i, int j){  
    if(i == -1 || j == -1){  
        return;  
    }  
    if(x[i] == y[j]){  
        PRINT_LCS(x, y, i-1, j-1);  
        printf("%c ", x[i]);  
    }else if(c[i-1][j] >= c[i][j-1]){  
        PRINT_LCS(x, y, i-1, j);  
    }else{  
        PRINT_LCS(x, y, i, j-1);  
    }  
}  
  
int main() {  
    char x[MAX] = "ABCBDAB", y[MAX] = "BDCABA";  
    LCS_LENGTH(x,y);  
    PRINT_LCS(x, y, strlen(x)-1, strlen(y)-1);  
    return 0;  
}

15.5 最优二叉搜索树

15.5.1 题目介绍

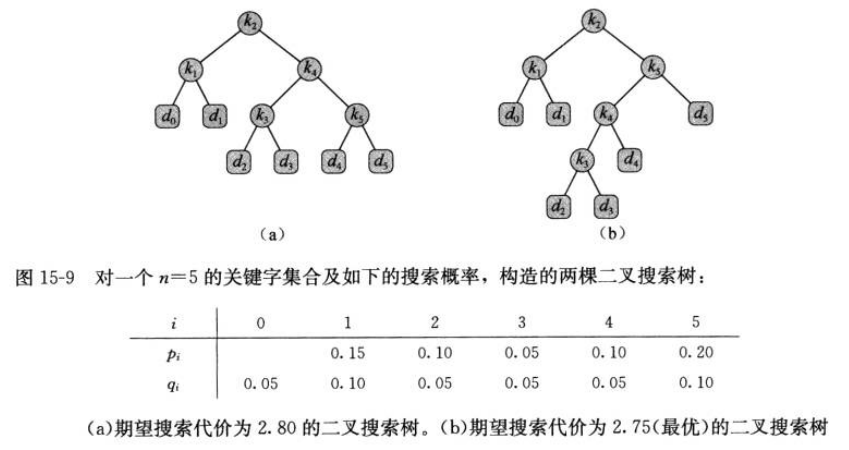
  • 最优二叉搜索树(optimal binary serach tree)问题：给定一个 个不同关键字的已排序的序列 因此 ，我们希望用这些关键字构造一棵二叉搜索树。对每个关键字 ，都有一个概率，表示其搜索频率。有些要搜索的值可能不在 中，因此我们还有 个 “伪关键字” 表示不在 中的值。 表示所有小于 的值， 表示所有大于 的值，对 ，，，，伪关键字 表示所有在 和 之间的值。对每个伪关键字 ，也都有一个概率 表示对应的搜索频率。下图显示了对一个 n=5 个关键字的集合构造的两棵二叉搜索树。每个关键字 是一个内部结点，而每个伪关键字 是一个叶结点。每次搜索要么成功（找到某个关键字 ）要么失败（找到某个为关键字 ），因此有如下公式：
  • Pasted image 20241015155651.png
  • 最优二叉搜索树：对于一个给定的概率集合，我们希望构造一棵期望搜索代价最小的二叉搜索树，我们称之为最优二叉搜索树
  • 穷举法获得最优二叉搜索树的时间复杂度为

15.5.2 思路&伪代码

步骤1：最优二叉搜索树的结构

给定关键字序列 ，其中某个关键字，比如说 ，是这些关键字的最优子树的根结点。那么 的左子树就包含关键字 （和伪关键字 ），而右子树包含关键字 （和伪关键字 ）。只要我们检査所有可能的根结点 ，并对每种情况分别求解包含 以及包含 的最优二叉搜索树，即可保证找到原问题的最优解。
特别的，我们认为包含关键字序列 的子树不含任何实际关键字，但包含单一伪关键字 。

步骤2：一个递归算法

选取子问题域为：求解包含关键字 的最优二叉搜索树，其中 且 （当时，子树不包含实际关键字，只包含伪关键字 ）。定义 为在包含关键字 的最优二叉搜索树中进行一次搜索的期望代价。最终，我们希望计算出 。
对于包含关键字 的子树，所有概率之和为 。
因此，若 为包含关键字 的最优二叉搜索树的根结点，我们有如下公式： 。
注意， 。
因此 可重写为
可得最终递归公式：

若若

并定义 保存根结点 的下标 。

步骤3：计算最优二叉搜索树的期望搜索代价

为提高效率，用 代替

其他

伪代码：接受概率列表 和 及规模 作为输入，返回表 和 。

OPTIMAL_BST(p, q, n)  
    let e[1..n+1,0..n],w[1..n+1,0..n],and root[1..n,1..n] be new tables  
    for i=1 to n+1  
        e[i,i-1] = q[i-1]  
        w[i,i-1] = q[i-1]  
    for l=1 to n  
        for i=1 to n-l+1  
            j = i+l-1  
            e[i,j] = ∞  
            w[i,j] = w[i,j-1]+p[j]+q[j]  
            for r=i to j  
                t = e[i,r-1]+e[r+1,j]+w[i,j]  
                if t<e[i,j]  
                    e[i,j] = t  
                    root[i,j] = r  
    return e and root

15.5.3 !c语言实现

复杂度： 

#include <stdio.h>  
  
#define MAX (1000+10)  
#define MAXE 1000000000  
double p[MAX], q[MAX], w[MAX][MAX], e[MAX][MAX];  
int root[MAX][MAX], n = 5;  
  
void optimalBST(double *p,double *q,int n);  
void printRoot();  
void printOptimalBST(int i,int j,int r);  
  
int main() {  
    scanf("%d", &n);  
    for(int i=1; i<=n; i++){  
        scanf("%lf", &p[i]);  
    }  
    for(int i=0; i<=n; i++){  
        scanf("%lf", &q[i]);  
    }  
    optimalBST(p,q,n);  
    printRoot();  
    printf("最优二叉树结构：\n");  
    printOptimalBST(1,n,-1);  
    return 0;  
}  
  
void optimalBST(double *p,double *q,int n){  
    // 初始化只包括虚拟键的子树  
    for (int i = 1;i <= n + 1;++i){  
        w[i][i - 1] = q[i - 1];  
        e[i][i - 1] = q[i - 1];  
    }  
  
    // 由上到下，由左到右逐步计算  
    for (int len = 1;len <= n;++len){  
        for (int i = 1;i <= n - len + 1;++i){  
            int j = i + len - 1;  
            e[i][j] = MAXE;  
            w[i][j] = w[i][j - 1] + p[j] + q[j];  
            // 求取最小代价的子树的根  
            for (int k = i;k <= j;++k){  
                double temp = e[i][k - 1] + e[k + 1][j] + w[i][j];  
                if (temp < e[i][j]){  
                    e[i][j] = temp;  
                    root[i][j] = k;  
                }  
            }  
        }  
    }  
}  
  
// 输出最优二叉查找树所有子树德根  
void printRoot(){  
    printf("各子树的根\n");  
    for (int i = 1;i <= n;++i){  
        for (int j = 1;j <= n;++j){  
            printf("%d ", root[i][j]);  
        }  
        puts("");  
    }  
    puts("");  
}  
  
// 打印最优二叉查找树的结构  
// 打印出[i,j]子树，它是根r的左子树和右子树  
void printOptimalBST(int i,int j,int r){  
    int rootChild = root[i][j];  
    if (rootChild == root[1][n]){  
        // 输出整棵树的根  
        printf("k%d是根\n", rootChild);  
        printOptimalBST(i,rootChild - 1,rootChild);  
        printOptimalBST(rootChild + 1,j,rootChild);  
        return;  
    }  
    if (j < i - 1){  
        return;  
    }else if (j == i - 1){      // 遇到虚拟键  
        if (j < r){  
            printf("d%d是k%d的左孩子\n", j, r);  
        }else {  
            printf("d%d是k%d的右孩子\n", j, r);  
        }  
        return;  
    }else{      // 遇到内部结点  
        if (rootChild < r){  
            printf("k%d是k%d的左孩子\n", rootChild, r);  
        }else{  
            printf("k%d是k%d的右孩子\n", rootChild, r);  
        }  
    }  
    printOptimalBST(i,rootChild - 1,rootChild);  
    printOptimalBST(rootChild + 1,j,rootChild);  
}
Built with MDFriday ❤️