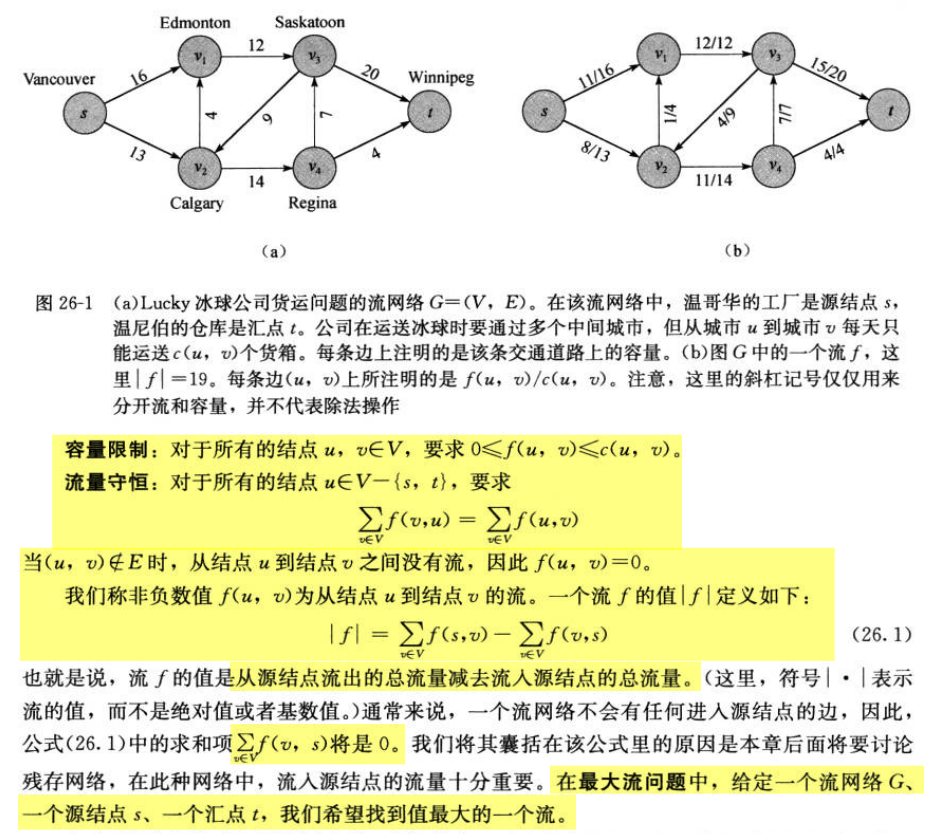
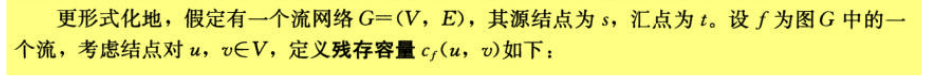1 流网络
1.1 基本定义
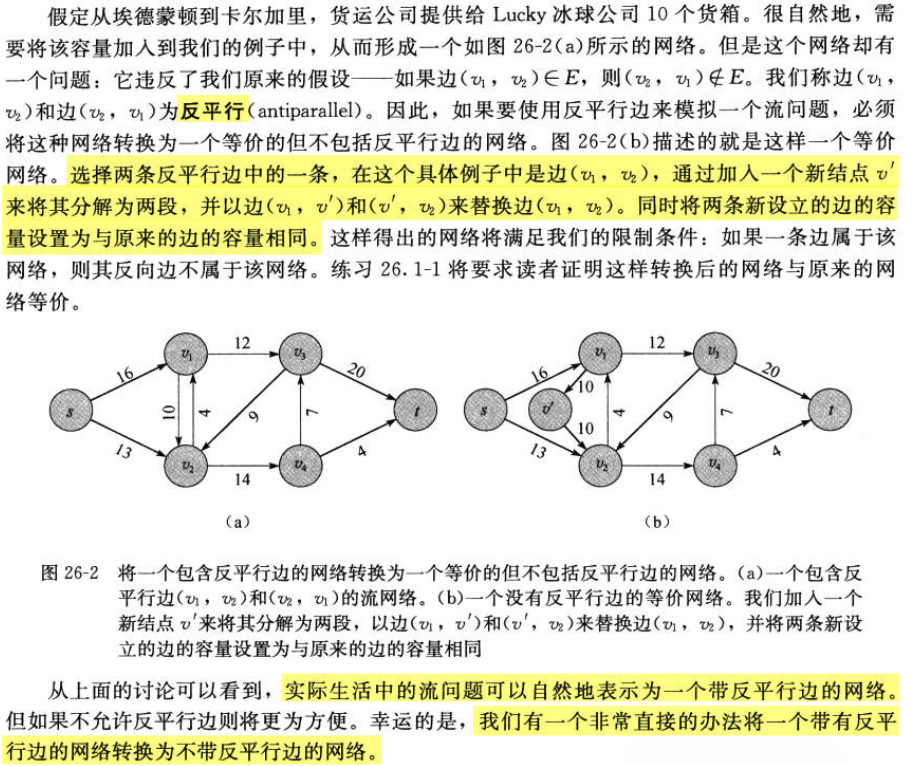
1.2 反平行边
增加新的点来分解到反平行的边
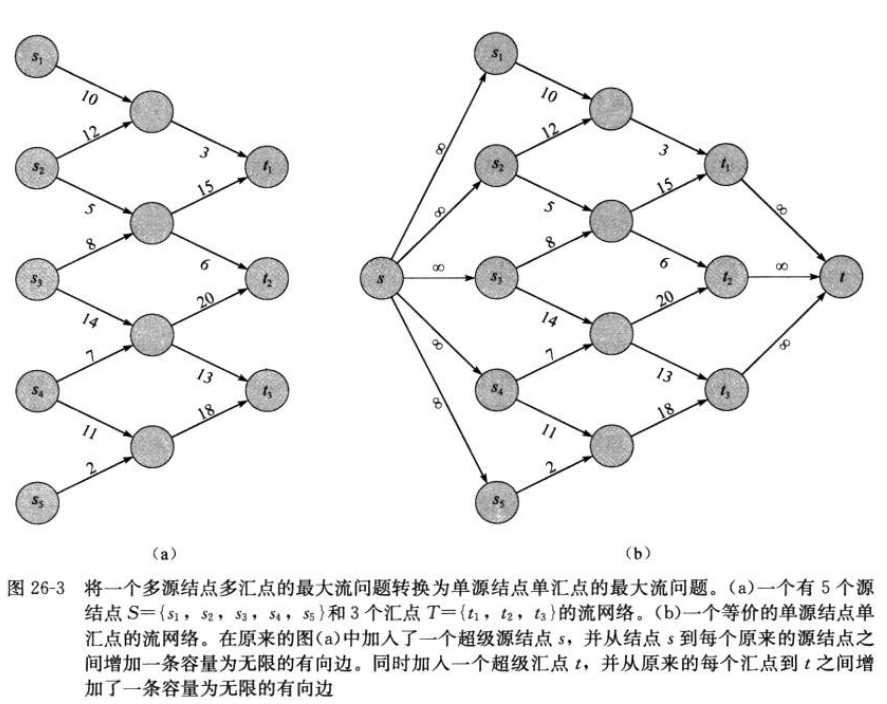
1.3 多个源节点和多个汇点
增加超级源结点和超级汇点
2 Ford-Fulkerson 方法
2.1 残存网络、增广路径、切割
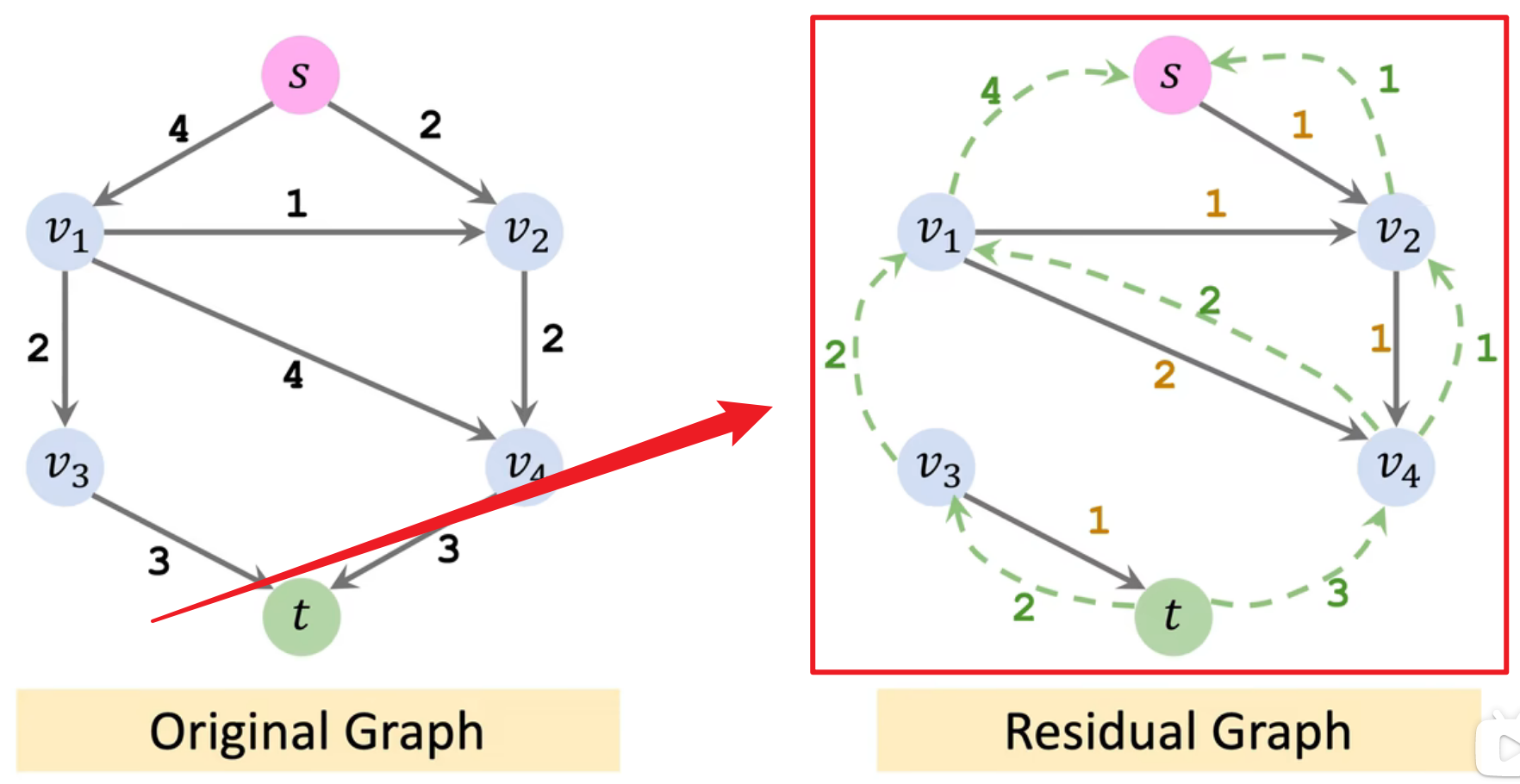
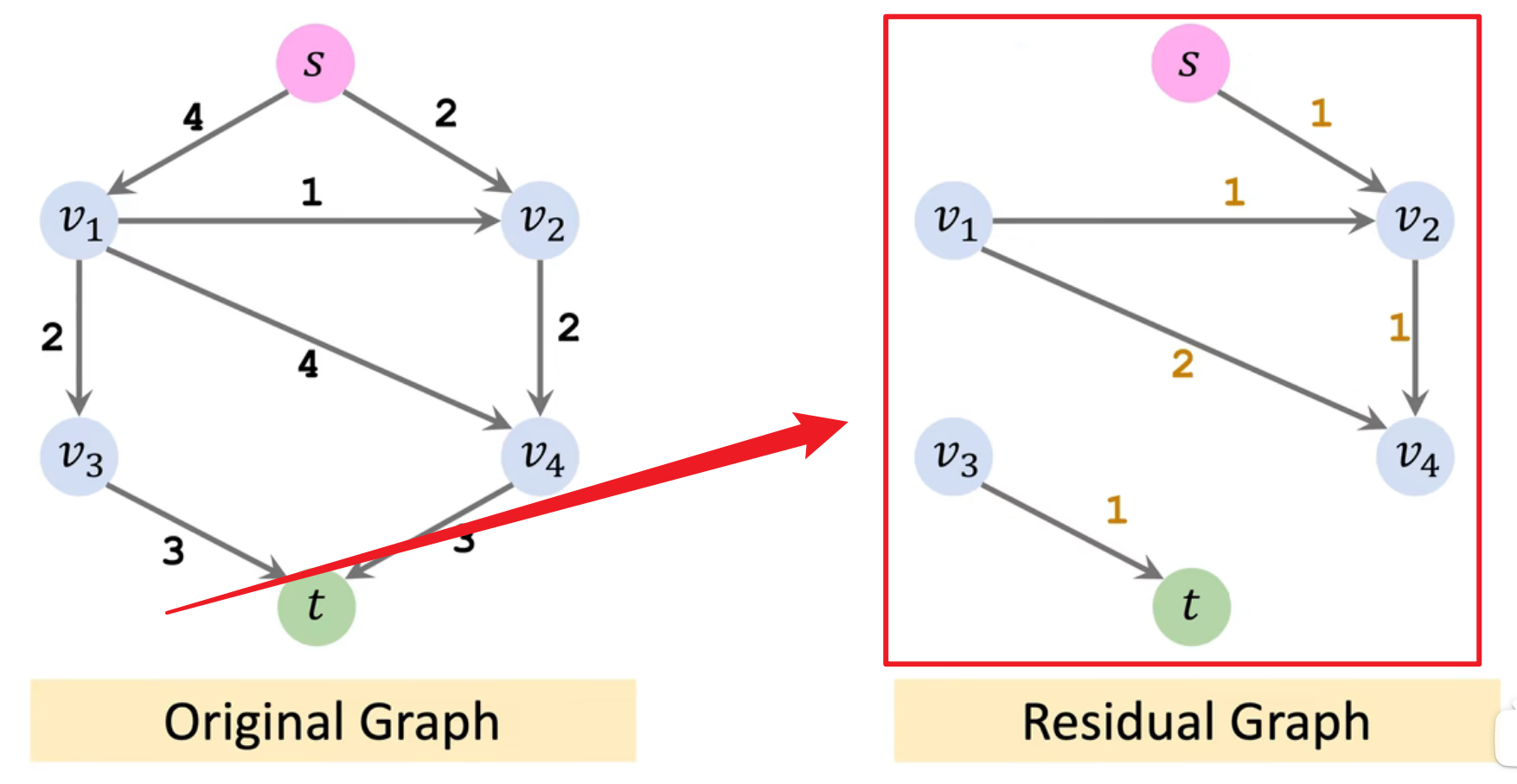
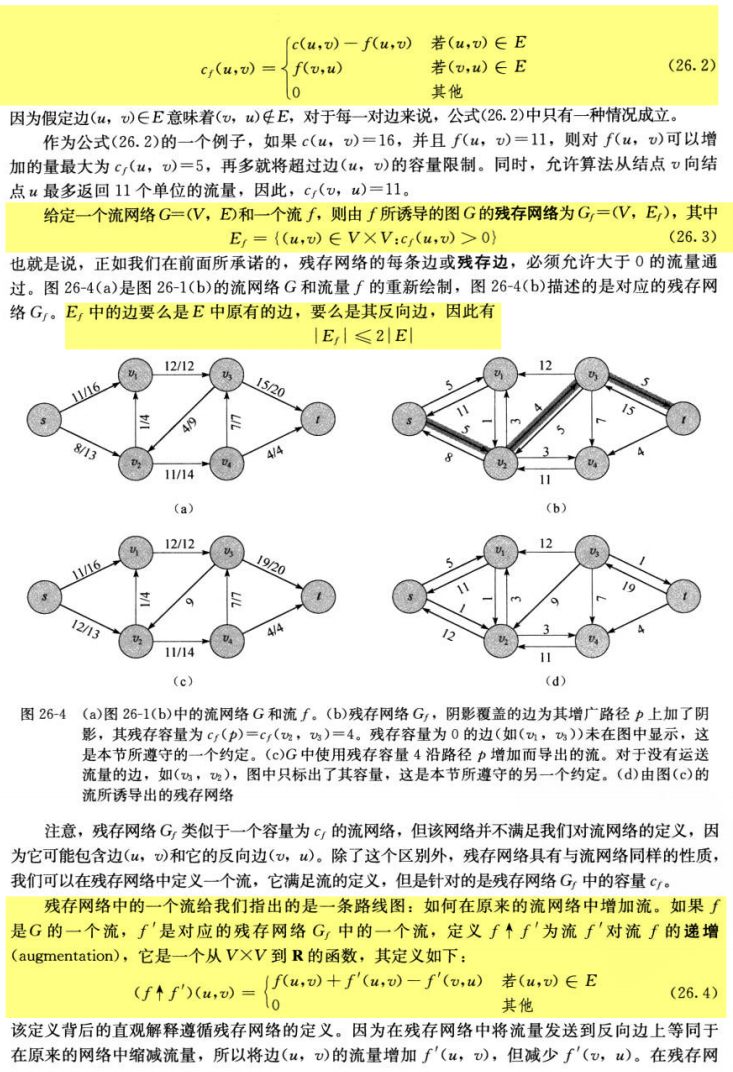
2.1.1 残存网络
- 残存网络用于跟踪流网络中每条边的剩余容量。每条边的剩余容量是指该边还能增加的最大流量。
2.1.2 增广路径(Augmenting Path)
- 增广路径是指从源点到汇点的一条路径,在这条路径上每条边的剩余容量都大于0。增广路径的目的是找到一条可以增加流量的路径,从而提高整个网络的流量。
2.1.3 流网络的切割
在流网络的Ford-Fulkerson方法中,流网络的切割(Cut)是指将网络中的顶点集分为两个不相交的子集,一个包含源点(source),另一个包含汇点(sink)。切割通常用一对顶点集(S, T)表示,其中S包含源点,T包含汇点,并且S和T的并集是网络中所有顶点的集合,S和T的交集为空。
切割的一个重要性质是,切割的容量(Cut Capacity)等于从S到T的所有边的容量之和。切割的容量限制了从S到T的流量,因为流量不能超过这些边的总容量。
在Ford-Fulkerson方法中,切割的概念用于证明最大流最小割定理(Max-Flow Min-Cut Theorem),该定理指出,对于任何流网络,最大流的值等于某个切割的最小容量。这个定理是流网络理论中的一个基本结果,它表明了最大流问题与最小割问题之间的等价性。
在算法的每一步中,Ford-Fulkerson方法通过寻找增广路径来增加流量,直到找不到增广路径为止。此时,残存图中的某个切割将源点和汇点分开,这个切割的容量就是当前流量的上限。由于最大流等于最小割,因此这个切割的容量也是网络的最大流值。
2.2 Ford-Fulkerson算法+伪代码
时间复杂度
2.3 Edmonds-Karp算法
在第3行的寻找增广路径的操作中使用广度优先搜索来改善效率,时间复杂度
2.3 !!!Edmonds-Karp cpp实现
#include <bits/stdc++.h>
using namespace std;
const int N=210;//边
const int INF=0x7FFFFFFF;
int n,m;
int map0[N][N]; //残留图,初始状态标识每条有向边的容量的图也可以看做是一个残留图
int pi[N]; //BFS的前驱图; pi[start]=0;pi[i]=-1,如果i没有在BFS中被扩展过
int flow_in[N]; //流入i的最大流量是flow_in[i]
int start,end0;
queue<int> q;
int bfs(){
int i,t;
while(!q.empty()) q.pop();
memset(pi,-1,sizeof(pi));
pi[start]=0;
flow_in[start]=INF; //key!
q.push(start);
while(!q.empty()){
t=q.front();
q.pop();
if(t==end0) break; // 已经走到汇点,循环结束
for(i=1;i<=m;i++){
if(pi[i]==-1 && map0[t][i]){ // 没遍历过点i且从t到i容量不为0
flow_in[i] = flow_in[t]<map0[t][i] ? flow_in[t] : map0[t][i]; // flow_in[i] = min(flow_in[t],map0[t][i])
q.push(i);
pi[i]=t; // i的前驱结点为t
}
}
}
if(pi[end0]==-1) return -1; //不存在增广路径
else return flow_in[m]; //还存在增光路径,不保证flow_in[m]达到最大可能值
}
int Edmonds_Karp(){
int max_flow_in=0; // 流f的流值|f|
int cf_p; // 增广路径的残留容量Cf(p)
int now,pre;
while((cf_p=bfs())!=-1){ // 当还有增广路径时
//1. 流值|f|增加本次增广路径的残留容量cf_p
max_flow_in+=cf_p;
//2. 顺着和逆着增广路径压入网络流
now=end0;
while(now!=start){
pre=pi[now];
map0[pre][now]-=cf_p; //更新正向边的实际容量
map0[now][pre]+=cf_p; //添加反向边
now=pre;
}
}
return max_flow_in;
}
int main(){
int i,u,v,cost;
while(scanf("%d%d",&n,&m)!=EOF){
memset(map0,0,sizeof(map0));//对于int[]/int[][],memset只能正常赋予0,-1两个值
for(i=0;i<n;i++){
scanf("%d%d%d",&u,&v,&cost);
map0[u][v]+=cost;
}
start=1,end0=m; // 1是源节点,m是汇点
printf("%d\n",Edmonds_Karp());
}
return 0;
}
2.4 !!!Dinic算法 cpp实现
- 第一行一个正整数 T(1≤T≤10),表示数据组数。
- 对于每组数据,第一行四个正整数 n,m,s,t(1≤n≤100,1≤m≤5×10^3,1≤s,t≤n),n个点,m条边,计算从s到t的最大流。
- 接下来 m 行,每行三个正整数 ui,vi,wi(1≤ui,vi≤n,0≤wi<2^31),表示第 i 条有向边 ui→vi 的最大容量为 wi。
- 图中有可能存在重边和自环。
#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
const int V_MAX = 205;
const int E_MAX = 5005;
const ll LL_INF = 0x3f3f3f3f3f3f3f3f;
ll max_stream = 0;
int cnt_E = 0;
int n, m, s, t;
struct Edge {
int to;
int nxt;
ll val;
} e[E_MAX * 2];
int head[V_MAX];
int depth[V_MAX];
void addEdge(int x, int y, int w);
void read();
bool bfs();
ll Dinic();
int main() {
ios::sync_with_stdio(false);
int T;
cin >> T;
while(T--){
cin >> n >> m >> s >> t;
cnt_E = 0, max_stream = 0;
fill(head + 1, head + 1 + n, -1);
/*----- 读入并初始化 -----*/
read();
cout << Dinic() << '\n';
}
return 0;
}
void addEdge(int x, int y, int w) {
e[cnt_E].to = y;
e[cnt_E].val = w;
e[cnt_E].nxt = head[x];
head[x] = cnt_E++;
}
void read() {
int u, v, w;
for (int i = 0; i < m; i++) {
cin >> u >> v >> w;
addEdge(u, v, w);
addEdge(v, u, 0);
}
}
bool bfs() {
memset(depth, 0, sizeof(depth));
depth[s] = 1;
queue<int> q;
q.push(s);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = head[u]; i > -1; i = e[i].nxt) {
int v = e[i].to;
if (e[i].val && !depth[v]) {
depth[v] = depth[u] + 1;
q.push(v);
}
}
}
if (depth[t] != 0)
return true;
return false;
}
ll dfs(int pos, ll in) {
if (pos == t)
return in;
ll out = 0;
for (int u = head[pos]; u > -1 && in; u = e[u].nxt) {
int v = e[u].to;
if (e[u].val && depth[v] == depth[pos] + 1) {
ll res = dfs(v, min(e[u].val, in));
e[u].val -= res;
e[u ^ 1].val += res;
in -= res;
out += res;
}
}
if (out == 0)
depth[pos] = 0;
return out;
}
ll Dinic() {
while (bfs())
max_stream += dfs(s, LL_INF);
return max_stream;
}
3 最大二分匹配
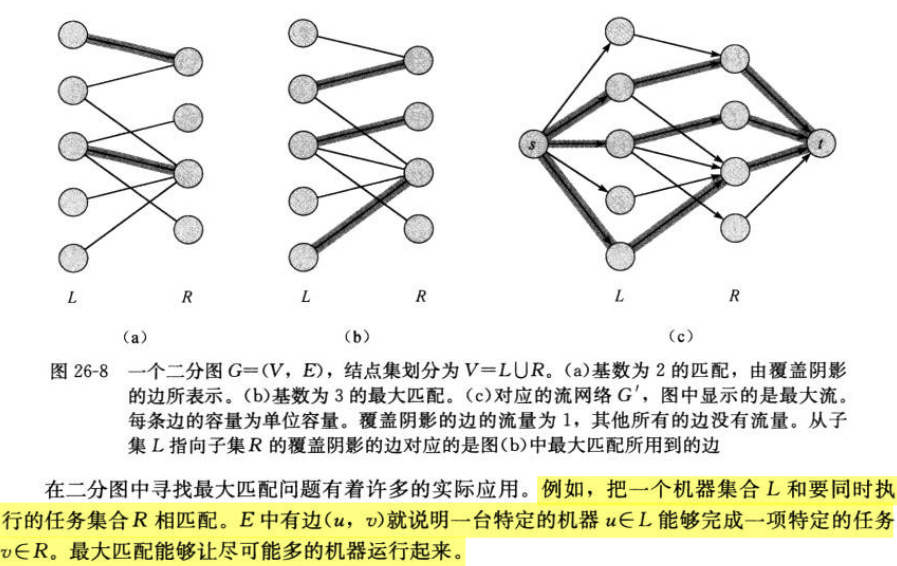
3.1 问题
左边一堆点,右边一堆点,左边的点都和点s(起始点)相连,右边的点都和点t(结束点)相连,左边的点和右边的点有的有边。求一种匹配方式,使得匹配的边数最多,其中每个顶点最多只能与一条边匹配。
3.2 乱七八糟的定理
3.3 !!!Dinic最小割 / 最大流 cpp实现
时间复杂度
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=510; // 最多有多少点
const int maxm=50050; // 最多有多少边
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,s,t,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void addedge(int u,int v,int cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs(){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front();
q.pop();
for(int i=0; i<tab[h].size(); i++){
edge &e=eg[tab[h][i]]; // 从h出发能到的边们
if(e.cap>e.flow && dis[e.v]==INF){ // 没遍历过点e.v且从h到e.v容量不为0
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow){
if(x==t||maxflow==0)
return maxflow;
int flow=0,f;
for(int i=cur[x]; i<tab[x].size(); i++){
cur[x]=i;
edge &e=eg[tab[x][i]]; // 从x出发能到的边们
if(dis[e.v]==dis[x]+1 && (f=dfs(e.v,min(maxflow,e.cap-e.flow)))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic(){
int flow=0;
while(bfs()){ // 还有增广路径的时候
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF);
}
return flow;
}
bool vis[555][555];
int main(){
int n,m,e,a,b;
scanf("%d%d%d", &n, &m, &e); // 左边点个数,右边点个数,总边数
tot=0, s=1001, t=1002; // s为起始点,t为终止点
for(int i=1; i<=n; i++) // 左边的点为1到n点,与s点有边
addedge(s,i,1);
for(int i=501; i<=500+m; i++)
addedge(i,t,1); // 右边的点为501到500+n点,与t点有边
while(e--){ // 还有边
scanf("%d%d",&a,&b); // 从点a到b有边
if(vis[a][b]) // a到b已经有边了,continue
continue;
vis[a][b] = true;
addedge(a,b+500,1); // a到b+500存边
}
printf("%d\n",dinic());
return 0;
}
3.4 匈牙利算法
匈牙利算法是基于深度优先搜索一遍一遍搜索增广路的存在性来增加匹配对数的。
我们将问题看作相亲现场,每个U集合的人排队寻找V集合里的对象。假设是男生排队找女生,基于这个"时间"顺序,假设前面的男生已经匹配了一些。
下一个男生a进来匹配,算法便会遍历一遍他认识的女生(与他有关系的VV集内的点)。如果发现当前遍历到的女生还没有被其他男生匹配,那非常好,就直接把这个女生匹配给男生a;如果发现已经被其他男生b给绿匹配了,那算法会尝试去和那个男生b沟通,询问能否让他换一个(?)
。算法便会来到那个男生b那里,重新遍历一遍他认识的女生,看看能否找到其他能够匹配的女生(寻找增广路/套娃)。如果可以,那么男生b便会与新找到的女生匹配,顺利成章的,原来与男生b匹配的女生就可以和男生a匹配啦。如果不行,那么男生a就没这个机会了QAQ,尝试下一个吧(继续遍历),实在不行(遍历完了)单着挺好的。
就以这样的方法一直搜索,直到所有男生(U集)该匹配的都匹配完了,就能得到最大匹配数了。
#include<bits/stdc++.h>
using namespace std;
const int N=555;
vector<int> G[N];
int match[N],vis[N];
// match用于存储谁(i)和谁(match[i])匹配
// vis用于存储当前这一边搜索是否已经让某个男生找过增广路了
bool used[N][N];
bool hungary(int p,int op){ // p表示第几个男生,op表示第几趟匹配
if(vis[p]==op)
return false;
vis[p]=op;
for(int i:G[p]){ // 对于每个男生p,遍历一遍他认识的女生
if(!match[i]||hungary(match[i],op)){
// 如果当前的女生没被匹配到,自然可以直接让她与当前的男生p进行匹配
// 但如果已经被匹配过,则尝试让匹配她的那个男生去再找找看其他女生(开始套娃),
// 如果返回true也可以正常匹配
match[i]=p;
return true;
}
}
return false;
}
int main(){
int n,m,e,a,b;
scanf("%d%d%d",&n,&m,&e);
while(e--){
scanf("%d%d",&a,&b);
if(used[a][b]) //判重边
continue;
used[a][b]=true;
G[a].push_back(b);
}
int ans=0;
for(int i=1;i<=n;i++)
if(hungary(i,i)) // 第i个男生,同时也是第i次搜寻
ans++;
printf("%d\n",ans);
return 0;
}