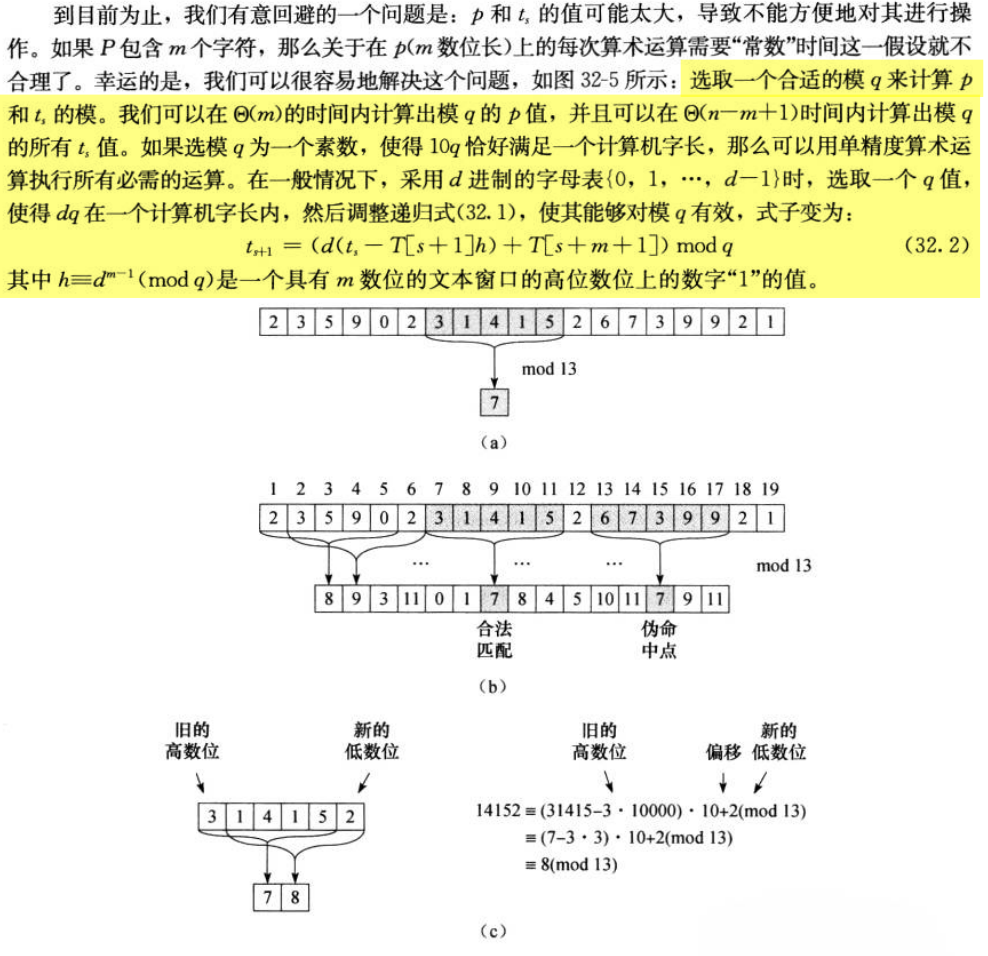
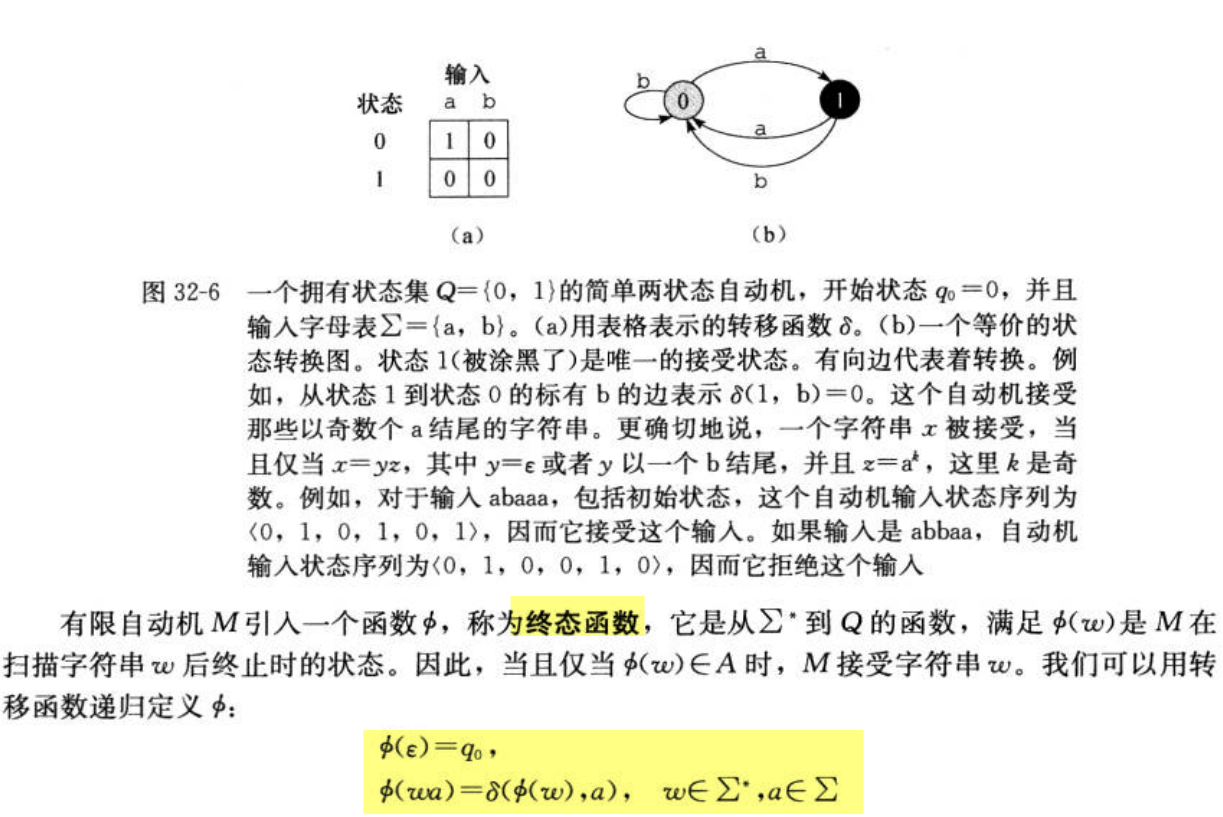
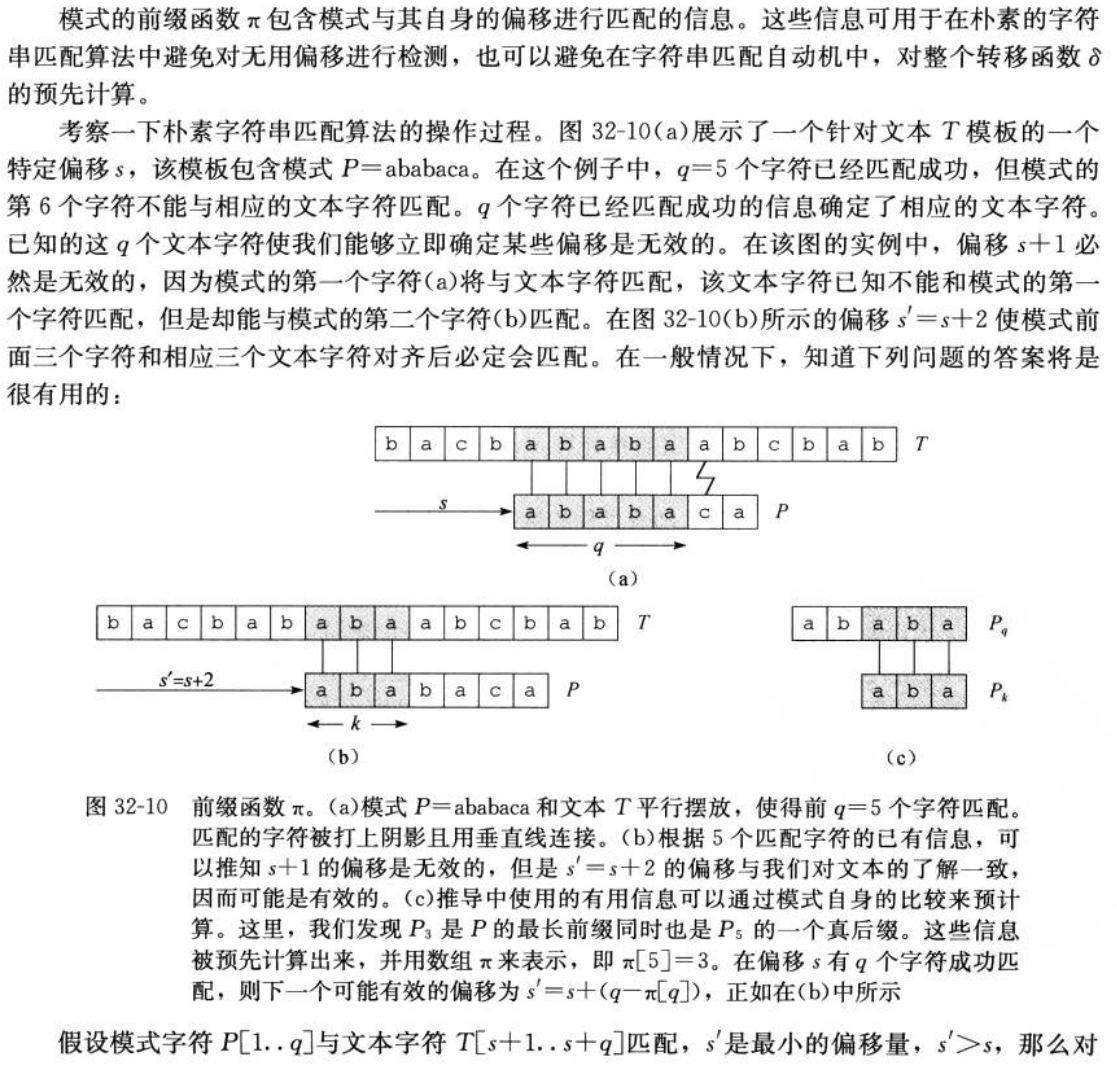
32.1 朴素字符串匹配算法

32.2 Rabin-Karp算法

理论

cpp实现

预处理时间 ，最坏运行时间 ，期望运行时间

// Rabin Karp Algorithm  
  
#include<iostream>  
#include<string>  
  
using namespace std;  
  
void Rabin_Karp_search(const string &T, const string &P, int d, int q){  
    int m = P.length();  
    int n = T.length();  
    int i, j;  
    int p = 0;  // hash value for pattern  
    int t = 0; // hash value for txt  
    int h = 1;  
    
    // The value of h would be "pow(d, M-1)%q"  
    for (i = 0; i < m-1; i++)  
        h = (h*d)%q;  
        
    // Calculate the hash value of pattern and first window of text  
    for (i = 0; i < m; i++)  {  
        p = (d*p + P[i])%q;  
        t = (d*t + T[i])%q;  
    }
    
    // Slide the pattern over text one by one  
    for (i = 0; i <= n - m; i++)  {  
    
        // Chaeck the hash values of current window of text and pattern  
        // If the hash values match then only check for characters on by one
        if ( p == t )  {  
            /* Check for characters one by one */  
            for (j = 0; j < m; j++)  
                if (T[i+j] != P[j])  
                    break;  
	            
            if (j == m)  // if p == t and pat[0...M-1] = txt[i, i+1, ...i+M-1]  
                cout<<"Pattern found at index :"<< i<<endl;  
        }  
  
        // Calulate hash value for next window of text: Remove leading digit,  
        // add trailing digit        
        if ( i < n-m ){  
            t = (d*(t - T[i]*h) + T[i+m])%q;  
            // We might get negative value of t, converting it to positive  
            if(t < 0)  
                t = (t + q);  
        }  
    }  
}  
  
int main()  {  
    string T = "Rabin–Karp string search algorithm: Rabin-Karp";  
    string P = "Rabin";  
    int q = 101;  // A prime number  
    int d = 16;  
    Rabin_Karp_search(T, P,d,q);  
//    system("pause");  
    return 0;  
}

32.3 字符串匹配有限自动机

理论

有限自动机

字符串匹配自动机

计算转移函数

cpp实现

#include <bits/stdc++.h>  
using namespace std;  
#include <string>  
#define total_chars 256  
#define trans_func(i, j) (trans_func[(i) * (m) + (j)])  
  
//using std::string;  
  
void transition(int* trans_func, string &pattern);  
  
void FSA(string &pattern, string &text) {  
    int m = pattern.length();  
    int n = text.length();  
    int* trans_func = new int[total_chars * m];  
    transition(trans_func, pattern);  
    int q = 0;  
    for (int i = 0; i < n; i++) {  
        q = trans_func(text[i], q);  
        if (q == m) {  
            printf("%d ", i-m+1);  
            q = 0;  
//            return i - m + 1;  
        }  
    }  
//    return -1;  
}  
  
void transition(int* trans_func, string &pattern) {  
    int m = pattern.length();  
    for (int i = 0; i < total_chars; i++) {  
        if (i == pattern[0]) {  
            trans_func(i, 0) = 1;  
        } else {  
            trans_func(i, 0) = 0;  
        }  
    }  
    int X = 0;  
    for (int j = 1; j < m; j++) {  
        for (int i = 0; i < total_chars; i++) {  
            if (pattern[j] == i) {  
                trans_func(i, j) = j + 1;  
            } else {  
                trans_func(i, j) = trans_func(i, X);  
            }  
        }  
        X = trans_func(pattern[j], X);  
    }  
}  
  
int main(){  
    string pattern = "abc";  
    string text = "abcabcdefghabc";  
    FSA(pattern, text);  
}

字母有限自动机模版 E6-D

#include <bits/stdc++.h>  
using namespace std;  
#include <string>  
#define total_chars 26  
#define trans_func(i, j) (trans_func[(i) * (m+1) + (j)])  
  
//using std::string;  
  
void transition(int* trans_func, string &pattern);  
  
void FSA(string &pattern) {  
    int m = pattern.length();  
    int* trans_func = new int[total_chars * (m+1)];  
    transition(trans_func, pattern);  
    long long ans = 0;  
    for(int j=0; j<=m; j++){  
        for (int i = total_chars*j+0; i < total_chars*j+total_chars; i++) {  
//            printf("%d ", trans_func[i]);  
            ans += trans_func[i];  
        }  
//        puts("");  
    }  
    printf("%lld", ans);  
//    return -1;  
}  
  
void transition(int* trans_func, string &pattern) {  
    int m = pattern.length();  
    for (int i = 0; i < total_chars; i++) {  
        if (i+'a' == pattern[0]) {  
            trans_func(i, 0) = 1;  
        } else {  
            trans_func(i, 0) = 0;  
        }  
    }  
    int X = 0;  
    for (int j = 1; j < m; j++) {  
//        printf("%d ", X);  
        for (int i = 0; i < total_chars; i++) {  
            if (pattern[j] == i+'a') {  
                trans_func(i, j) = j + 1;  
            } else {  
                trans_func(i, j) = trans_func(i, X);  
            }  
        }  
        X = trans_func(pattern[j]-'a', X);  
    }  
    if(X == m-1){  
        for (int i = 0; i < total_chars; i++) {  
            trans_func(i, m) = m;  
        }  
    }else{  
        for (int i = 0; i < total_chars; i++) {  
            if (pattern[X] == i+'a') {  
                trans_func(i, m) = X + 1;  
            } else {  
                trans_func(i, m) = trans_func(i, X);  
            }  
        }  
    }  
//    puts("");  
}  
  
int main(){  
    string pattern;  
    cin >> pattern;  
    FSA(pattern);  
}

32.4 Knuth-Morris-Pratt算法

理论

关于模式的前缀函数

前缀函数计算的正确性

KMP算法的正确性

cpp实现

时间复杂度

#include <iostream>  
#include <vector>  
#include <string>  
  
using namespace std;  
  
vector<int> prefix(string str);  
  
int main(){  
    string text;  
    string key;  
    cin >> text;  
    cin >> key;  
    int kl = key.length();  
    vector<int> kmp = prefix(key);  
    int k = 0;  
    for(int i = 0; i < text.length(); i++){  
        while (k && key[k] != text[i])  
            k = kmp[k - 1];  
        if(text[i] == key[k])  
            k++;  
        if(k == kl)  
            cout << i - k + 2 << endl;  
    }  
    for(auto x: kmp)  
        cout << x << " ";  
    return 0;  
}  
vector<int> prefix(string str){  
    int l = (int) str.length();  
    vector<int> pre(l);  
    for(int i = 1; i < l; i++){  
        int j = pre[i - 1];     // i-1的最大的前缀==后缀  
        while (j && str[j] != str[i])   // 如果 j>0(防止死循环) 且 i-1的最大的前缀==后缀 的最后一个字跟当前的后缀的最后一个字不同  
            j = pre[j - 1];     // ababaababab  
        if(str[j] == str[i])  
            j++;  
        pre[i] = j;  
    }  
    return pre;  
}

// 求π函数
#include <iostream>  
#include <vector>  
#include <string>  
  
using namespace std;  
  
vector<int> prefix(string str);  
  
int main(){  
    string key;  
    cin >> key;  
    vector<int> kmp = prefix(key);  
    for(auto x: kmp)  
        cout << x << " ";  
    return 0;  
}  
vector<int> prefix(string str){  
    int l = (int) str.length();  
    vector<int> pre(l);  
    for(int i = 1; i < l; i++){  
        int j = pre[i - 1];     // i-1的最大的前缀==后缀  
        while (j && str[j] != str[i])   // 如果 j>0(防止死循环) 且 i-1的最大的前缀==后缀 的最后一个字跟当前的后缀的最后一个字不同  
            j = pre[j - 1];     // ababaababab  
        if(str[j] == str[i])  
            j++;  
        pre[i] = j;  
    }  
    return pre;  
}