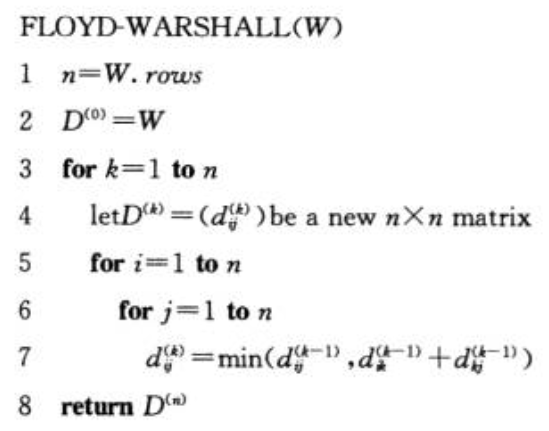2 floyd算法

2.1 简介

2.2 伪代码

2.3 cpp实现

空间复杂度

#include <stdio.h>  
#include <limits.h>  
  
#define V 310  // 图中节点的数量  
long long dist[V][V], graph[V][V], Path[V][V];  // dist数组：距离distance graph数组：图  
  
// 佛洛依德算法的实现  
void floydWarshall() {  
    // 初始化最短路径矩阵  
    for (int i = 0; i < V; i++)  
        for (int j = 0; j < V; j++){  
            if(graph[i][j] != 0){  
                dist[i][j] = graph[i][j];  
            }else{  
                dist[i][j] = LONG_LONG_MAX;  
            }  
            if(dist[i][j] < LONG_LONG_MAX && i != j){  
                Path[i][j] = j;  
            }else{  
                Path[i][j] = -1;  
            }  
        }  
  
    // 更新最短路径矩阵  
    for (int k = 0; k < V; k++) {  
        for (int i = 0; i < V; i++) {  
            for (int j = 0; j < V; j++) {  
                if (dist[i][k] != LONG_LONG_MAX && dist[k][j] != LONG_LONG_MAX && dist[i][k] + dist[k][j] < dist[i][j]) {  
                    dist[i][j] = dist[i][k] + dist[k][j];  
                    Path[i][j] = k;    // k是从i到j的途经点
                }  
            }  
        }  
    }  
}  

// 打印最短路径
void PrintPath(long long u, long long v){  
    printf("%lld ", u);  
    while(Path[u][v] != v){  
        printf("%lld ", Path[u][v]);  
        u = Path[u][v];  
    }  
    printf("%lld\n", v);  
}  
  
int main() {  
    int n, m;  
    scanf("%d%d", &n, &m);  
    for(int i=0; i<m; i++){  
        long long u, v, w;  
        scanf("%lld%lld%lld", &u, &v, &w);  
        if((graph[u][v]!=0 && w<graph[u][v]) || graph[u][v] == 0){  // 考虑到可能有重复边  
            graph[u][v] = w;  
        }  
    }  
    floydWarshall();  
  
    int q;  // q次询问  
    scanf("%d", &q);  
    while(q--){  
        int u, v;  
        scanf("%d%d", &u, &v);  
        if(u == v){     // u和v是同一个点，距离为0  
            printf("%d->%d: 0\n", u, v);  
        }else if(dist[u][v] == LONG_LONG_MAX){  // u不可达v，输出-1  
            printf("%d->%d:-1\n", u, v);  
        }else{  // u可达v
            printf("%d->%d:%lld\n", u, v, dist[u][v]);  
            PrintPath(u, v);  
        }  
    }  
    return 0;  
}

2.4 有向图的传递闭包

• 传递闭包： ，其中 如果图中包含一条从结点到结点的路径
  用于解决问题：给定有向图，判断对于所有结点对i和j，图G是否包含一条从结点i到结点j的路径

2.4.1 法1:floyd算法每条边权重赋1

时间复杂度：

2.4.2 法2

时间复杂度：，但用逻辑或、逻辑与代替min和+，可一定程度上减少时间

#include <stdio.h>  
  
#define V 310  // 图中节点的数量  
long long dist[V][V];  // dist数组：距离distance graph数组：图  
  
// 佛洛依德算法的实现  
void floydWarshall() {  
    // 初始化最短路径矩阵  
    for (int i = 0; i < V; i++)  
        dist[i][i] = 1;  
  
    // 更新最短路径矩阵  
    for (int k = 0; k < V; k++) {  
        for (int i = 0; i < V; i++) {  
            for (int j = 0; j < V; j++) {  
                dist[i][j] = dist[i][j] | (dist[i][k] & dist[k][j]);  
            }  
        }  
    }  
}  
  
int main() {  
    int n, m;  
    scanf("%d%d", &n, &m);  
    for(int i=0; i<m; i++){  
        long long u, v, w;  
        scanf("%lld%lld%lld", &u, &v, &w);  
        dist[u][v] = 1;  
    }  
    floydWarshall();  
  
    int q;  // q次询问  
    scanf("%d", &q);  
    while(q--){  
        int u, v;  
        scanf("%d%d", &u, &v);  
        if(dist[u][v]){     // u可达v，输出1  
            printf("%d->%d: 1\n", u, v);  
        }else{  // u不可达v，输出0  
            printf("%d->%d: 0\n", u, v);  
        }  
    }  
    return 0;  
}

2.5 经过固定点的最短路