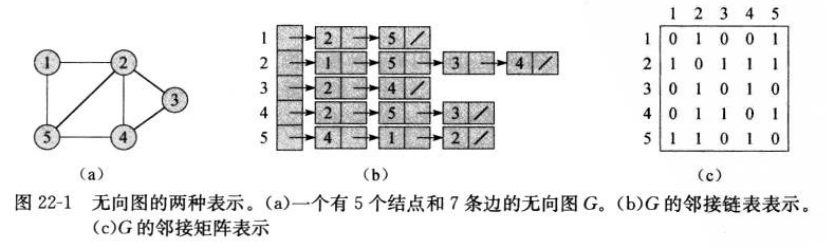
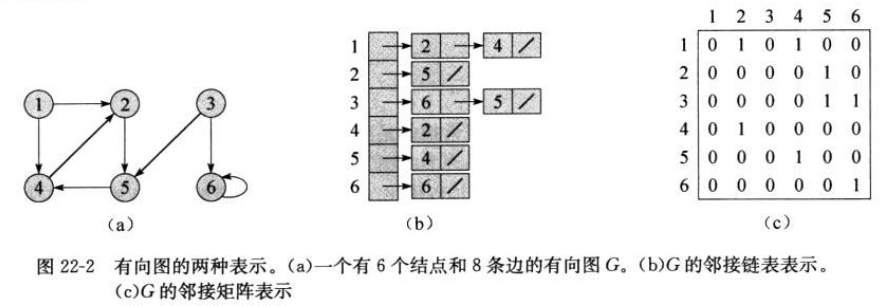
1 图的表示

稀疏图：边的条数远远小于的图
稠密图：接近的图
权重图
表示方法：
- 邻接链表：存储空间，有向图的邻接链表长度之和等于，无向图的邻接链表长度之和等于
- 邻接矩阵：存储空间，

2 广度优先搜索

2.1 BFS

u.color
白色：还未被“发现”
黑色：子节点都被发现完
灰色：其他
u.π：前驱节点
u.d：从s到u的距离

BFS(G,s)

for each vertex u \in G.V-{s}
	u.color = WHITE
	u.d = INF
	u.π = NIL
s.color = GRAY
s.d = 0
s.π = NIL
Q = ∅
enqueue(Q, s)
while Q \neq ∅
	u = dequeue(Q)
	for each v \in G.Adj[u]
		v.color = GRAY
		v.d = u.d + 1
		v.π = u
		enqueue(Q, v)
	u.color = BLACK

2.2 最短路径

Pasted image 20241029001433.png
Pasted image 20241029001447.png
Pasted image 20241029001503.png
Pasted image 20241029001516.png
Pasted image 20241029001525.png
Pasted image 20241029001552.png

printPath(G, s, v)

if v==s
	print s
else if v.π == NIL
	print "no path from" s "to" v "exists"
else
	printPath(G, s, v.π)
	print v

2.3 cpp实现

2.3.1 邻接矩阵

#include <bits/stdc++.h>  
#define MaxV (10000+10)  
  
using namespace std;  
  
int G[MaxV][MaxV];        // 邻接矩阵  
bool visited[MaxV];  
int last[MaxV], d[MaxV];  
  
void BFS(int i, int n);  
void printPath(int s, int v);  
  
int main(){  
    int n, m;  
    scanf("%d%d", &n, &m);  
    for(int i=0; i<m; i++){  
        int u, v;  
        scanf("%d%d", &u, &v);  
        G[u][v] = 1;  
    }  
    
    BFS(1, n);  
	for(int i=2;i<n;i++){   // 如果是非连通图，该循环保证每个极大连通子图中的顶点都能被遍历到     
		if(!visited[i])  
		    DFS(i,n);  
	}
    puts("");  
    printPath(1, 4);  
    puts("");  
    printf("%d", d[4]);  
    return 0;  
}  
  
void BFS(int i, int n){  
    queue<int> Q;   // 队列  
  
    Q.push(i);  // 当前节点  
    visited[i] = true;  // 当前节点被visited过了  
    printf("v%d->", i);  
  
    while(!Q.empty()){  
        int k = Q.front();  
        Q.pop();  
        for(int j=1; j<=n; j++){  
            if(G[k][j] == 1 && !visited[j]){  
                Q.push(j);  // 当前节点  
                visited[j] = true;  // 当前节点被visited过了  
                printf("v%d->", j);  
                d[j] = d[k]+1;  
                last[j] = k;  
            }  
        }  
    }  
}  
  
void printPath(int s, int v){  
    if(v == s){  
        printf("%d ", s);  
    }else if(last[v] == 0){  
        printf("No path from %d to %d exists", s, v);  
    }else{  
        printPath(s, last[v]);  
        printf("%d ", v);  
    }  
}

2.3.2 邻接表

#include <bits/stdc++.h>  
#define MaxV (10000+10)  
  
using namespace std;  
  
typedef struct edge{       // 定义边结点类型  
    int adjvex;  
    int weight;  
    struct edge *next;  
}ELink;  
typedef struct ver{       // 定义顶点结点类型  
    int vertex;  
    ELink* link;  
}VLink;  
  
VLink G[MaxV];  
bool visited[MaxV];  
int last[MaxV], d[MaxV];  
  
void BFS(int i, int n);  
void printPath(int s, int v);  
  
int main(){  
    int n, m;  
    scanf("%d%d", &n, &m);  
    for(int i=0; i<m; i++){  
        int u, v;  
        scanf("%d%d", &u, &v);  
        ELink* e = (ELink*) malloc(sizeof (ELink));  
        e->adjvex = v, e->weight = 0, e->next = nullptr;  
        if(G[u].link == nullptr){  
            G[u].link = e;  
        }else{  
            e->next = G[u].link;  
            G[u].link = e;  
        }  
    }  
    BFS(1, n);
    for(int i=2;i<n;i++){   // 如果是非连通图，该循环保证每个极大连通子图中的顶点都能被遍历到     
	    if(!visited[i])  
		    BFS(i,n);  
	}
    puts("");  
    printPath(1, 4);  
    puts("");  
    printf("%d", d[4]);  
  
    return 0;  
}  
  
void BFS(int i, int n){  
    queue<int> Q;   // 队列  
    ELink* p;  
  
    Q.push(i);  // 当前节点  
    visited[i] = true;  // 当前节点被visited过了  
    printf("v%d->", i);  
  
    while(!Q.empty()){  
        int k = Q.front();  
        Q.pop();  
        p = G[k].link;  
  
        while(p != nullptr){    // 如果队列头结点非空  
            int j = p->adjvex;  // 头结点序号  
            if(!visited[j]){    // 没visited过当前节点  
                printf("v%d->", j);  
                visited[j] = true;  
                Q.push(j);  
                d[j] = d[k]+1;  
                last[j] = k;  
            }  
            p = p->next;    // 下个节点  
        }  
    }  
}  
  
void printPath(int s, int v){  
    if(v == s){  
        printf("%d ", s);  
    }else if(last[v] == 0){  
        printf("No path from %d to %d exists", s, v);  
    }else{  
        printPath(s, last[v]);  
        printf("%d ", v);  
    }  
}

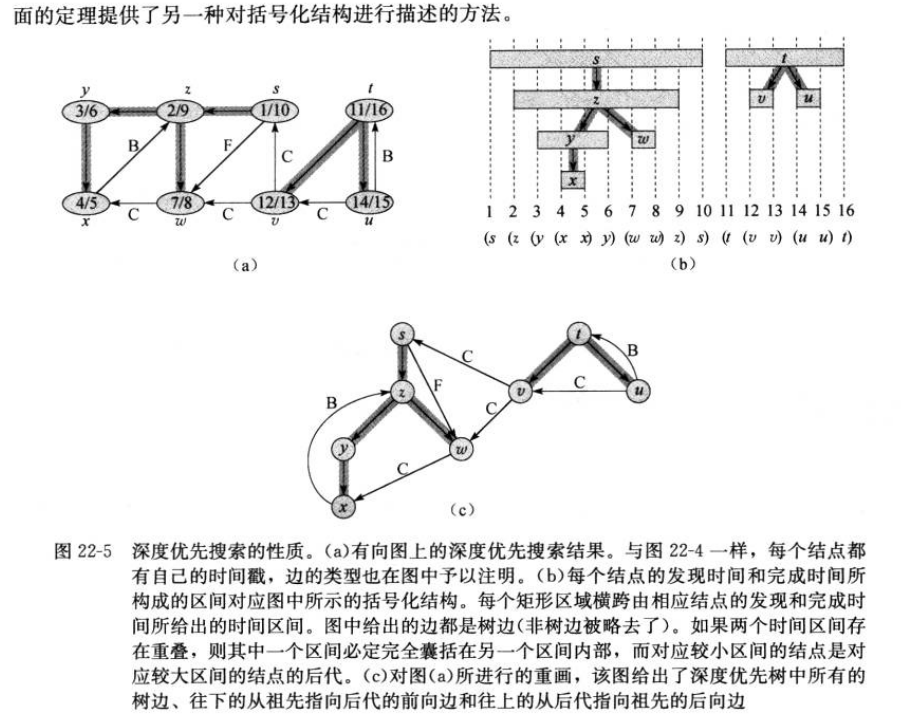
3 深度优先搜索

3.1 伪代码

Pasted image 20241029093553.png

u.color
白色：还未被“发现”
黑色：子节点都被发现完
灰色：其他
u.π：前驱节点
u.d：u第一次被发现的时间
u.f：完成对u的邻接链表扫描的时间

DFS(G)

for each vertex u \in G.V
	u.color = WHITE
	u.π = NIL
time = 0
for each vertex u \in G.V
	if u.color == WHITE
		DFS_VISIT(G, u)

DFS_VISIT(G, u)

time = time+1    // u被发现了
u.d = time
u.color = GRAY
for each v \in G:Adj[u]    // explore edge (u, v)
	if v.color == WHITE
		u.π = u
		DFS_VISIT(G,v)
u.color = BLACK   // blacken u as it is finished
time = time+1
u.f = time

3.2 性质

Pasted image 20241029093940.png
Pasted image 20241029093950.png
Pasted image 20241029094000.png
Pasted image 20241029094009.png
Pasted image 20241029094017.png
Pasted image 20241029094027.png
Pasted image 20241029094035.png
Pasted image 20241029094043.png

3.3 cpp实现

3.3.1 邻接矩阵

时间复杂度

#include <bits/stdc++.h>  
#define MaxV (10000+10)  
  
using namespace std;  
  
int G[MaxV][MaxV];        // 邻接矩阵  
bool visited[MaxV];  
int last[MaxV], d[MaxV];  
  
void DFS(int i, int n);  
void printPath(int s, int v);  
  
int main(){  
    int n, m;  
    scanf("%d%d", &n, &m);  
    for(int i=0; i<m; i++){  
        int u, v;  
        scanf("%d%d", &u, &v);  
        G[u][v] = 1;  
    }  
  
    DFS(1, n);  
    for(int i=2;i<n;i++){   // 如果是非连通图，该循环保证每个极大连通子图中的顶点都能被遍历到         
	    if(!visited[i])  
	        DFS(i,n);  
    }  
    puts("");  
    printPath(1, 4);  
    puts("");  
    printf("%d", d[4]); 
    return 0;  
}  
  
void DFS(int i, int n){  
    printf("v%d->", i);  
    visited[i] = true;  
    for(int j=1; j<=n; j++){  
        if(G[i][j] == 1 && !visited[j]){
	        last[j] = i;
            d[j] = d[i]+1;
            DFS(j, n);
        }  
    }  
}  
  
void printPath(int s, int v){  
    if(v == s){  
        printf("%d ", s);  
    }else if(last[v] == 0){  
        printf("No path from %d to %d exists", s, v);  
    }else{  
        printPath(s, last[v]);  
        printf("%d ", v);  
    }  
}

3.3.2 邻接表

时间复杂度

#include <bits/stdc++.h>  
#define MaxV (10000+10)  
  
using namespace std;  
  
typedef struct edge{       // 定义边结点类型  
    int adjvex;  
    int weight;  
    struct edge *next;  
}ELink;  
typedef struct ver{       // 定义顶点结点类型  
    int vertex;  
    ELink* link;  
}VLink;  
  
VLink G[MaxV];  
bool visited[MaxV];  
int last[MaxV], d[MaxV];  
  
void DFS(int i, int n);  
void printPath(int s, int v);  
  
int main(){  
    int n, m;  
    scanf("%d%d", &n, &m);  
    for(int i=0; i<m; i++){  
        int u, v;  
        scanf("%d%d", &u, &v);  
        ELink* e = (ELink*) malloc(sizeof (ELink));  
        e->adjvex = v, e->weight = 0, e->next = nullptr;  
        if(G[u].link == nullptr){  
            G[u].link = e;  
        }else{  
            e->next = G[u].link;  
            G[u].link = e;  
        }  
    }  
    DFS(1, n);  
    for(int i=2;i<n;i++){   // 如果是非连通图，该循环保证每个极大连通子图中的顶点都能被遍历到     
	    if(!visited[i]) 
            DFS(i,n);  
    }  
    puts("");  
    printPath(1, 4);  
    puts("");  
    printf("%d", d[4]);  
  
    return 0;  
}  
  
void DFS(int i, int n){  
    ELink* p;  
    printf("v%d->", i);  
    visited[i] = true;  
    p = G[i].link;  
  
    while(p != NULL){  
        int j = p->adjvex;  
        if(!visited[j]){  
            last[j] = i;  
            d[j] = d[i]+1;  
            DFS(j, n);  
        }  
        p = p->next;  
    }  
}  
  
void printPath(int s, int v){  
    if(v == s){  
        printf("%d ", s);  
    }else if(last[v] == 0){  
        printf("No path from %d to %d exists", s, v);  
    }else{  
        printPath(s, last[v]);  
        printf("%d ", v);  
    }  
}

4 拓扑排序

4.1 简介

Pasted image 20241030092129.png
Pasted image 20241030092144.png
Pasted image 20241030092156.png

4.2 伪代码

Pasted image 20241030092210.png

4.3 cpp实现

#include <bits/stdc++.h>  
using namespace std;  
  
// 定义图的最大顶点数  
#define MAX_VERTICES 10010  
  
// 定义图的结构  
unordered_map<int, vector<int>>graph;  
  
struct Edge {         //链式前向星，存边的起点、终点、和前驱  
    int x, y, next;  
} e[MAX_VERTICES];  
  
int cnt;          //存储的边数  
  
int main() {  
    int t;  
    scanf("%d", &t);  
    while(t--){  
        int head[MAX_VERTICES] = {};       //下标是起点的表头，存第一个边的编号，初始化为 -1        int id[MAX_VERTICES]={};          //每个点的入度  
        graph.clear();  
  
        int n, m;  
        cnt = 1;  
        scanf("%d%d", &n, &m);  
          
        // 读入  
        for (int i = 1; i <= m; i++) {  
            int x,y;  
            scanf("%d%d", &x, &y);  
  
            e[cnt].x = x;              //起点  
            e[cnt].y = y;              //终点  
            e[cnt].next = head[x];     //添加  
            id[y]++;  
            head[x] = cnt++;          //更新表头  
            graph[x].push_back(y);  
        }  
  
        // 拓扑排序  
        queue<int> q;      //队列  
        for (int i = 1; i <= n; i++) {  
            if (id[i] == 0)  
                q.push(i);        //把入度为0的点入队  
        }  
        vector<int> ans;              //数组保存结果  
        while (!q.empty()) {  
            int x = q.front();         //出队  
            q.pop();  
            ans.push_back(x);  
            int edge = head[x];  
            while (edge != 0) {  
                id[e[edge].y]--;       //删除边  
                if (id[e[edge].y] == 0) //把入度为0的点入队  
                    q.push(e[edge].y);  
                edge = e[edge].next;  
            }  
        }  
  
        // 输出形成的拓扑序列  
        for(int an : ans){  
            printf("%d ", an);  
        }  
  
    }  
    return 0;  
}