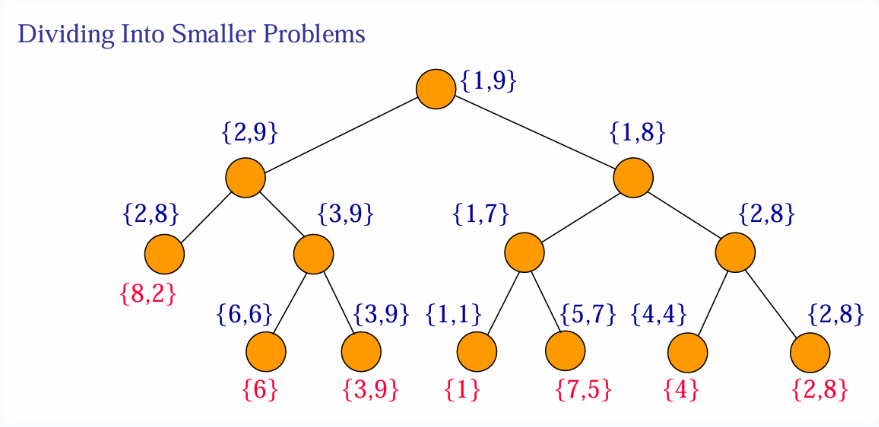
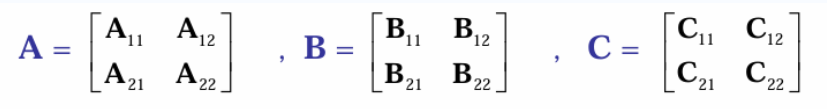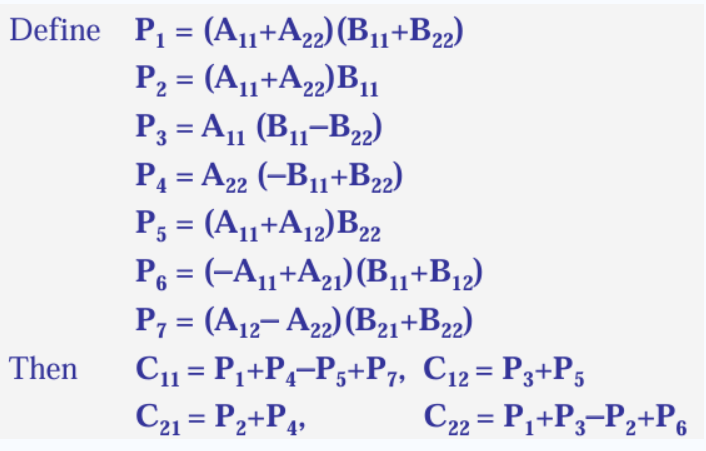1 例:整数相乘
写一个不被卡精度的多项式乘法-开始玩karatsuba algorithm - 知乎 (zhihu.com)
(超简单、超易懂、超详细)算法精讲(四十二):卡拉次巴乘法-CSDN博客
2 例:矩阵相乘
Strassen算法(斯特拉森算法),求C=A\times B
其中
有
3 例:找MaxMin
例:多数问题
n个数组成一个数组,寻找是否有一个数的数量≥n/2
```c
#include <stdio.h>
const int N = 2000000; //定义数组的最大长度
int a[N];
int majorityDC(int a[], int start, int end, int result) {
//分治法求解多数问题,数组下标区间为[start, end]
if (start == end) {
result = a[end];
return 1;
}else{
int m1, m2;
majorityDC(a, start, (start + end) / 2, &m1);
//m1为前半区间[start, (start + end) / 2]的多数
majorityDC(a, (start + end) / 2 + 1, end, &m2);
//m2为后半区间[(start + end) / 2 + 1, end]的多数
int count1 = 0, count2 = 0;
for (int i = start; i <= end; i++) {
if (a[i] == m1) { //count1记录m1在数组a[]中出现的次数
count1++;
}
if (a[i] == m2) { //count2记录m2在数组a[]中出现的次数
count2++;
}
}
if(count1 > ((end - start + 1) / 2)) {
//m1在数组a[]中出现的次数大于数组长度的一半,则m1为多数
result = m1;
return 1;
}else if(count2 > ((end - start + 1) / 2)) {
//m2在数组a[]中出现的次数大于数组长度的一半,则m2为多数
result = m2;
return 1;
}else{
return 0; //m1, m2均不是多数,则数组a[]的多数不存在
}
}
}
int main() {
int n, resultDC;
scanf("%d", &n);
for(int i=0; i<n; i++){
scanf("%d\n", &a[i]);
}
if(majorityDC(a, 0, n - 1, &resultDC)){
printf("%d", resultDC);
}else{
printf("Can not find the majority!");
}
return 0;
}