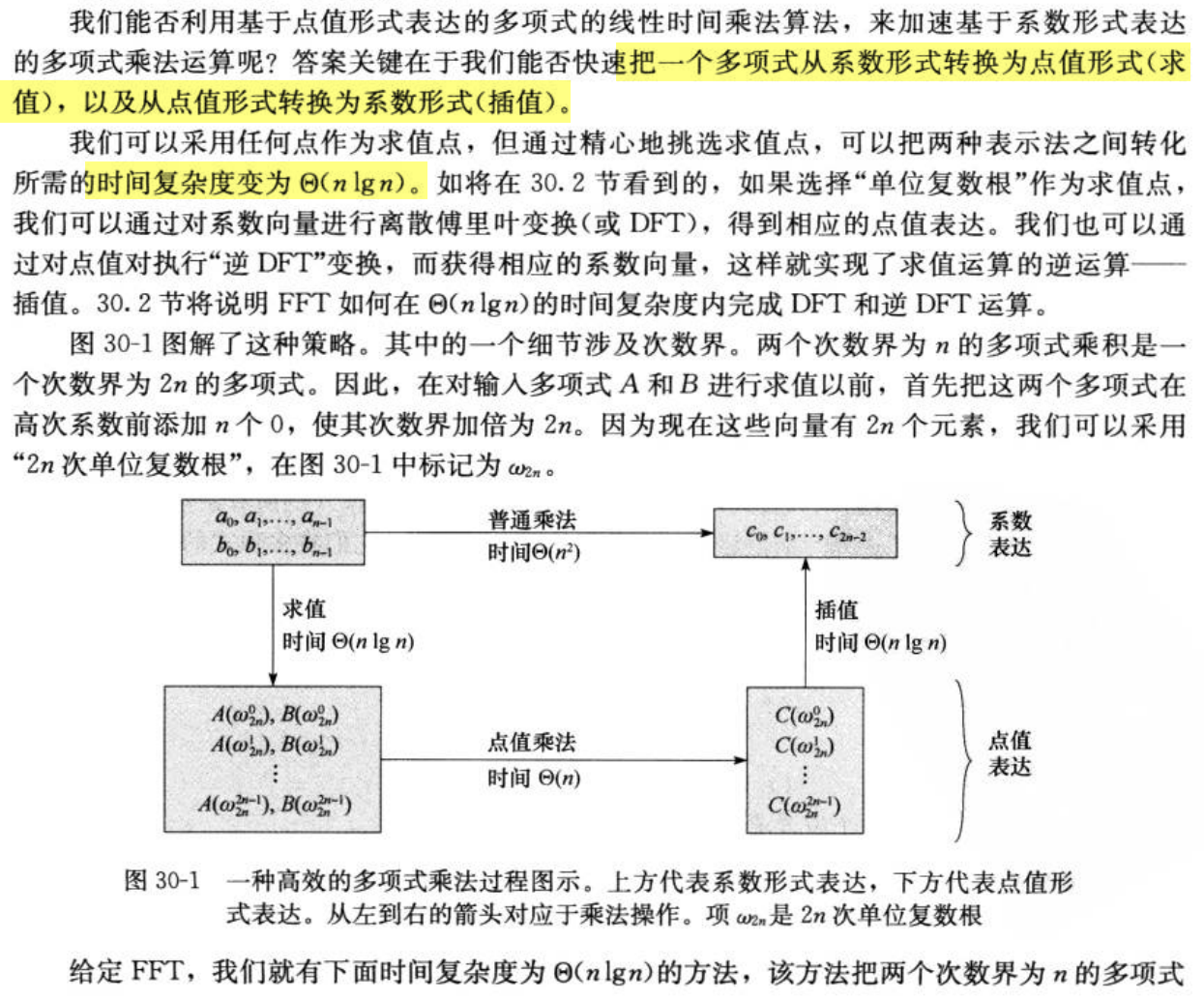
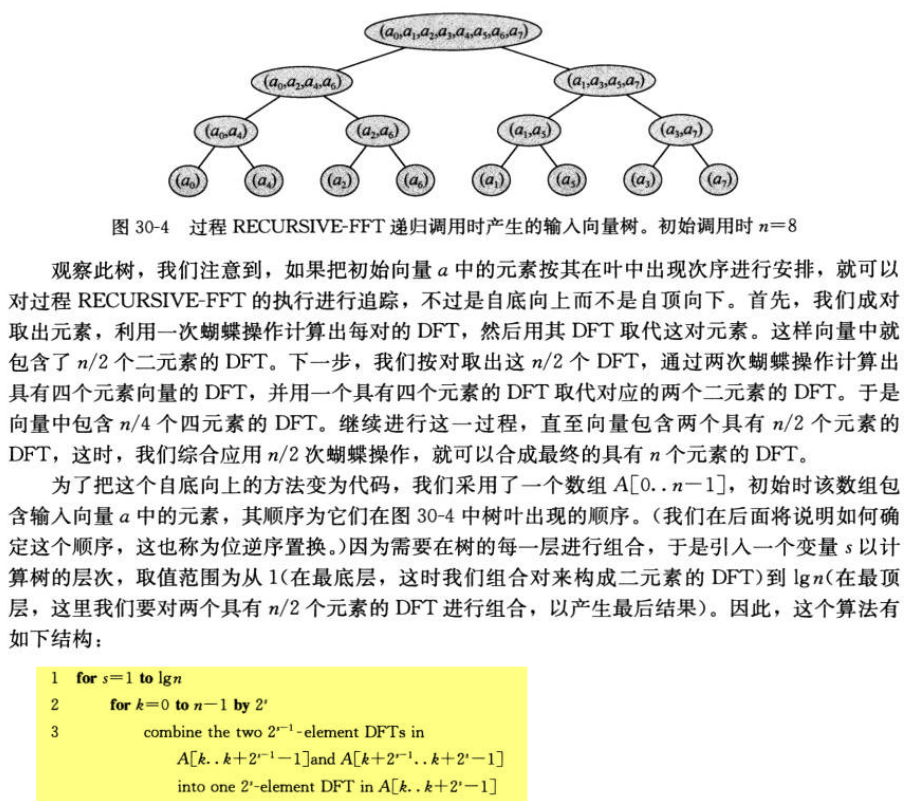
30.1 多项式的表示

30.1.1 系数表达

30.1.2 点值表达

插值多项式的唯一性（定理30.1）：任意n个点值， 各不相同，存在唯一的次数界为n的多项式 ，满足

运用拉格朗日公式求解A的所有系数

设有  个点，坐标为 ， 现在要求解它们所够成的  次多项式  的系数。
先回顾一下一般拉格朗日插值：

 必须满足代入任意一个 ， 得到一个对应的 。

因此
可以通过构造得
那么
现在我们得到
考虑如何得到  的系数，可以先 ， 求得 这个多项式的所有系数。
但是我们发现这并不满足  这个条件，因此要想办法对每个  除去 ，这就要用到多项式除法。又因为  的系数为 ，因此单次除法可以做到 。这样，我们就可以对每个 ，每次  得到分子，而分母的  只与  有关，因此需要每次重新算。
然后，对每个 ，我们将  得到的分子乘上分母的逆元，再乘上 ，就得到了  的一部分（它也是个多项式）。
最后，再将所有  得到的系数值对应相加就得到了 。
总时间复杂度为 。

#include<bits/stdc++.h>  
using namespace std;  
const int N=2e3+5,MOD=998244353;  
int n,X[N],Y[N],fz1[N],fz2[N],tmp[N],xs[N];  
int ksm(int x,int y){  
    int res=1;  
    while(y){  
        if(y&1)res=1ll*res*x%MOD;  
        x=1ll*x*x%MOD;  
        y>>=1;  
    }  
    return res;  
}  
inline int inc(int x,int y){return (x+y>=MOD)?(x+y-MOD):(x+y);}  
inline int dec(int x,int y){return (x-y<0)?(x-y+MOD):(x-y);}  
void pmul(int *A,int deg,int xi){//系数从下标1开始,deg表示多项式的度数  
    for(int i=deg+1;i>=1;i--)  
        tmp[i]=A[i],A[i]=A[i-1];  
    for(int i=1;i<=deg+1;i++)  
        A[i]=inc(A[i],1ll*tmp[i]*xi%MOD);  
}  
void pdiv(int *A,int *res,int deg,int xi){  
    for(int i=1;i<=deg+1;i++)tmp[i]=A[i];  
    for(int i=deg;i>=1;i--)  
        res[i]=tmp[i+1],tmp[i]=dec(tmp[i],1ll*tmp[i+1]*xi%MOD);  
}  
int main(){  
    // n个点  
    scanf("%d",&n);  
    for(int i=1;i<=n;i++)  
        scanf("%d%d",&X[i],&Y[i]);  
    fz1[1]=1;  
    for(int i=1;i<=n;i++)  
        pmul(fz1,i,dec(0,X[i]));  
    for(int i=1;i<=n;i++){  
        int fm=1;  
        for(int j=1;j<=n;j++)  
            if(i!=j)fm=1ll*fm*dec(X[i],X[j])%MOD;  
        pdiv(fz1,fz2,n,dec(0,X[i]));  
        fm=1ll*Y[i]*ksm(fm,MOD-2)%MOD;  
        for(int j=1;j<=n;j++)  
            xs[j]=inc(xs[j],1ll*fm*fz2[j]%MOD);  
    }  
    // 按次数从小到大输出系数  
    for(int i=1;i<=n;i++)  
        printf("%d ",xs[i]);  
    return 0;  
}

30.1.3 系数形式表示的多项式的快速乘法（FFT引入）

30.2 DFT与FFT

30.2.1 理论

1 单位复数根

2 DFT

3 FFT

4 在单位复数根处插值

30.2.2 cpp实现

时间复杂度

#include <iostream>  
#include <vector>  
#include <cmath>  
  
const double Pi = acos(-1);  
const int MAX = 4000005;  
using namespace std;  
typedef long long ll;  
  
struct Complex {  
	double x, y;  
	Complex operator+(const Complex &b) const {  
		return {x + b.x, y + b.y};  
	}  
	  
	Complex operator-(const Complex &b) const {  
		return {x - b.x, y - b.y};  
	}  
	  
	Complex operator*(const Complex &b) const {  
		return {x * b.x - y * b.y, x * b.y + y * b.x};  
	}  
} f[MAX], p[MAX], sav[MAX];  
void dft(Complex *f, int len);  
  
void idft(Complex *f, int len);  
  
int main() {  
	int n, m;  
	cin >> n >> m;  // 第一个多项式最多n次，第二个最多m次
	for (int i = 0; i <= n; i++)  
		cin >> f[i].x;  // 读入第一个多项式的系数
	for (int i = 0; i <= m; i++)  
		cin >> p[i].x;  // 读入第二个多项式的系数
	for (m += n, n = 1; n <= m; n <<= 1);  // 相乘最多n+m位
	dft(f, n);  
	dft(p, n);  
	for (int i = 0; i < n; i++)  
		f[i] = f[i] * p[i];  
	idft(f, n);  
	for (int i = 0; i <= m; i++)  
		cout << (int) (f[i].x / n + 0.49) << " ";  // 四舍五入
	return 0;  
}  
  
void dft(Complex *f, int len) {  
	if (len == 1)  
		return;  
	Complex *fl = f, *fr = f + len / 2;  
	for (int k = 0; k < len; k++)  
		sav[k] = f[k];  
	for (int k = 0; k < len / 2; k++) {  
		fl[k] = sav[k << 1];  
		fr[k] = sav[k << 1 | 1];  
	}  
	dft(fl, len / 2);  
	dft(fr, len / 2);  
	Complex tG = {cos(2 * Pi / len), sin(2 * Pi / len)};  // omega_n
	Complex buf = {1, 0};  // omega
	for (int k = 0; k < len / 2; k++) {  
		sav[k] = fl[k] + buf * fr[k];  
		sav[k + len / 2] = fl[k] - buf * fr[k];  
		buf = buf * tG;  // omega = omega*omega_n
	}  
	for (int k = 0; k < len; k++)  
		f[k] = sav[k];  
}  
  
void idft(Complex *f, int len) {  
	if (len == 1)  
		return;  
	Complex *fl = f, *fr = f + len / 2;  
	for (int k = 0; k < len; k++)  
		sav[k] = f[k];  
	for (int k = 0; k < len / 2; k++) {  
		fl[k] = sav[k << 1];  
		fr[k] = sav[k << 1 | 1];  
	}  
	idft(fl, len / 2);  
	idft(fr, len / 2);  
	Complex tG = {cos(2 * Pi / len), -sin(2 * Pi / len)};  
	Complex buf = {1, 0};  
	for (int k = 0; k < len / 2; k++) {  
		sav[k] = fl[k] + buf * fr[k];  
		sav[k + len / 2] = fl[k] - buf * fr[k];  
		buf = buf * tG;  
	}  
	for (int k = 0; k < len; k++)  
		f[k] = sav[k];  
}

30.3 高效FFT实现

理论

cpp实现

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000000 + 7;
#define PI acos(-1)
int n,m;
complex<double> a[maxn*3], b[maxn*3];
int pos[maxn*3];
void FFT(complex<double>*A, int len, int type){
	for(int i=0; i<len; i++){//把每个数放到最后的位置
		if(i<pos[i])
			swap(A[i], A[pos[i]]);//保证每对只交换一次
	}
	for(int L=2; L<=len; L<<=1){//循环合并的区间长度
		int HLen = L/2;//区间的一半
		complex<double> Wn (cos(2.0*PI/L), type*sin(2.0*PI/L));
		for(int R=0; R<len; R+=L){//每个小区间的起点
			complex<double> w(1,0);
			for(int k=0; k<HLen; k++, w=w*Wn){//求该区间下的值
				complex<double> Buf = A[R+k];//蝴蝶操作，去掉odd和even数组，使变化原地进行
				A[R+k] =  A[R+k] + w*A[R+k+HLen];
				A[R+k+HLen] = Buf - w*A[R+k+HLen];
			}
		}
	}
}
int main(){
    int x;pos[0] = 0;
    int maxLen = 1, l = 0;
    scanf("%d%d", &n, &m);
    while(maxLen < n+m+1){
	    maxLen<<=1;
	    l++;
	}
    for(int i = 0;i<=n;i++){
        scanf("%d",&x);
        a[i].real(x);
    }
    for(int i = 0;i<=m;i++){
        scanf("%d",&x);
        b[i].real(x);
    }
    for(int i = 0;i<maxLen;i++){//求最后交换的位置（奇数特殊处理）
        pos[i] = (pos[i>>1]>>1)|((i&1)<<(l-1));
    }
    
    FFT(a,maxLen,1);
    FFT(b,maxLen,1);
    for(int i = 0;i<maxLen;i++)
	    a[i]*=b[i];
    
    FFT(a,maxLen,-1);
    
    for(int i = 0;i<n+m+1;i++){
        if(i!=0) printf(" ");
        printf("%d",(int)(a[i].real()/maxLen+0.5));
    }
    printf("\n");
    return 0;
}