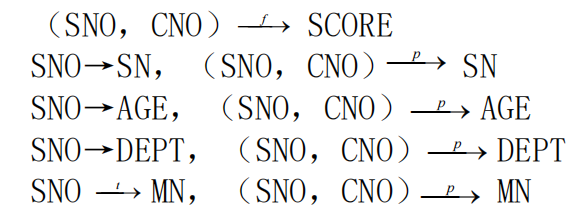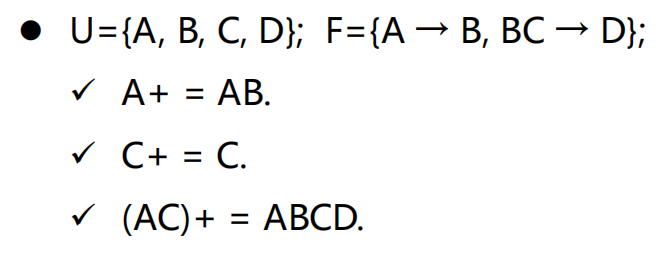11 关系数据理论

什么是规范化理论

在关系数据库系统中，关系模型包括一组关系模式，各个关系不是完全孤立的，数据库的设计较层次和网状模型更为重要。

一个好的关系数据库模式应该包括多少关系模式，而每一个关系模式又应该包括哪些属性，又如何将这些相互关联的关系模式组建一个适合的关系模型，这些工作决定了整个系统运行的效率，也是系统成败的关键所在，所以必须在关系数据库的规范化理论的指导下逐步完成

规范化理论的主要内容

函数信赖
范式（Normal Form）
模式分解
其中，函数信赖起着核心的作用，是模式分解和模式设计的基础，范式是模式分解的标准。

规范化问题的提出

数据库的逻辑设计为什么要遵循一定的规范化理论？
什么是好的关系模式？
某些不好的关系模式可能导致哪些问题？

参考下面例子

要求设计教学管理数据库，设计出来的关系模式SCD如下：SCD(SNO,SN,AGE,DEPT,MN,CNO,SCORE)
其中，SNO表示学生学号，SN表示学生姓名，AGE表示学生年龄，DEPT表示学生所在的系别，MN表示系主任姓名，CNO表示课程号，SCORE表示成绩。

会出现

数据冗余
例如每个系名和系主任的名字存储的次数等于该系的学生人数乘以每个学生选修的课程门数，同时学生的姓名、年龄也都要重复存储多次，数据的冗余度很大，浪费了存储空间

插入异常
如果某个新系没有招生，尚无学生时，则系名和系主任的信息无法插入到数据库中。
因为在这个关系模式中，(SNO,CNO)是主键。根据关系的实体完整性约束，主键的值不能为空，而这时没有学生，SNO和CNO均无值，因此不能进行插入操作。另外，当某个学生尚未选课，即CNO未知，实体完整性约束还规定，主键的值不能部分为空，同样不能进行插入操作。

删除异常
某系学生全部毕业而没有招生时，删除全部学生的记录则系名、系主任也随之删除，而这个系依然存在，在数据库中却无法找到该系的信息。
另外，如果某个学生不再选修C1课程，本应该只删去C1，但C1是主关系键的一部分，为保证实体完整性，必须将整个元组一起删掉，这样，有关该学生的其它信息也随之丢失。

更新异常
如果学生改名，则该学生的所有记录都要逐一修改SN；
又如某系更换系主任，则属于该系的学生记录都要修改MN的内容，稍有不慎，就有可能漏改某些记录，这就会造成数据的不一致性，破坏了数据的完整性。

由于存在以上问题，我们说，SCD是一个不好的关系模式。产生上述问题的原因，直观地说，是因为关系中“包罗万象” ，内容庞杂且互相影响。那么，什么样的才是一个好的关系模式呢？

我们把关系模式SCD分解为下面三个结构简单的关系模式：

学生关系S(SNO,SN,AGE,DEPT)

选课关系SC(SNO,CNO,SCORE)

系关系D(DEPT,MN)
在以上三个关系模式中，实现了信息的某种程度的分离.
分解后的关系模式是一个好的关系数据库模式。

从而得出结论，一个好的关系模式应该具备以下四个条件：

尽可能少的数据冗余。
没有插入异常。
没有删除异常。
没有更新异常。

如何按照一定的规范设计关系模式，将结构复杂的关系分解成结构简单的关系，从而把不好的关系数据库模式转变为好的关系数据库模式，这就是关系的规范化。
规范化又可以根据不同的要求而分成若干级别。（还要考虑跨表查询很慢）
我们要设计的关系模式中的各属性是相互依赖、相互制约的，这样才构成了一个结构严谨的整体。
因此在设计关模式时，必须从语义上分析这些依赖关系。
数据库模式的好坏和关系中各属性间的依赖关系有关，因此，我们先讨论属性间的依赖关系，然后再讨论关系规范化理论

1 函数依赖

函数依赖的定义

关系模式中的各属性之间相互依赖、相互制约的联系称为数据依赖。
数据依赖一般分为函数依赖、多值依赖和连接依赖。
其中，函数依赖是最重要的数据依赖。

函数依赖（Functional Dependency）是关系模式中属性之间的一种逻辑依赖关系。

例如在上一节介绍的关系模式SCD中，SNO与SN、AGE、DEPT之间都有一种依赖关系。
由于一个SNO只对应一个学生，而一个学生只能属于一个系，所以当SNO的值确定之后，SN，AGE，DEPT的值也随之被唯一的确定了
这类似于变量之间的单值函数关系。设单值函数Y=F(X)，自变量X的值可以决定一个唯一的函数值Y。
在这里，我们说SNO决定函数（SN，AGE，DEPT），或者说 （SN，AGE，DEPT）函数依赖于SNO。

函数依赖的形式化定义
设关系模式R(U，F)，U是属性全集，F是U上的函数依赖集，X和Y是U的子集，如果对于R(U)的任意一个可能的关系r，对于X的每一个具体值，Y都有唯一的具体值与之对应，则称X决定函数Y，或Y函数依赖于X，记作X→Y。我们称X为决定因素，Y为依赖因素。当Y不函数依赖于X时，记作： $⇸$ 。当且时，则记作：。

例
对于关系模式SCD U={SNO,SN,AGE,DEPT,MN,CNO,SCORE}

很显然：SNO→SN，SNO→AGE，SNO→DEPT

一个SNO有多个SCORE的值与其对应，因此SCORE不能唯一地确定，即SCORE不能函数依赖于SNO，所以有：SNO ⇸ SCORE。

但是SCORE可以被（SNO，CNO）唯一地确定。所以可表示为：（SNO，CNO）→SCORE。

（SNO，CNO,AGE）→SCORE

有关函数依赖的几点说明

平凡的函数依赖与非平凡的函数依赖
- 当属性集Y是属性集X的子集时，则必然存在着函数依赖X→Y，这种类型的函数依赖称为平凡(Trivial)的函数依赖。（SNO，CNO）→SNO
- 如果Y不是X的子集，则称X→Y为非平凡的函数依赖。
- 若不特别声明，我们讨论的都是非平凡的函数依赖。
.函数依赖是语义范畴的概念
- 我们只能根据语义来确定一个函数依赖，而不能按照其形式化定义来证明一个函数依赖是否成立。
- 例如，对于关系模式S，当学生不存在重名的情况下，可以得到
  SN→AGE
  SN→DEPT
- 这种函数依赖关系，必须是在没有重名的学生条件下才成立的，否则就不存在函数依赖了。
- 所以函数依赖反映了一种语义完整性约束。
函数依赖关系的存在与时间无关
- 因为函数依赖是指关系中的所有元组应该满足的约束条件，而不是指关系中某个或某些元组所满足的约束条件。
- 当关系中的元组增加、删除或更新后都不能破坏这种函数依赖。
- 因此，必须根据语义来确定属性之间的函数依赖，而不能单凭某一时刻关系中的实际数据值来判断。
函数依赖可以保证关系分解的无损连接性
- 设R（X，Y，Z），X，Y，Z为不相交的属性集合，如果X→Y或X→Z，则有R(X，Y，Z) = R1[X，Y] ⋈ R2[X，Z]
- 其中，R1[X，Y]表示关系R在属性（X，Y）上的投影
- 即R等于其投影在X上的自然连接，这样便保证了关系R分解后不会丢失原有的信息，称作关系分解的无损连接性。
- 基于上述原则的分解方法称为投影分解
例如，对于关系模式SCD，有SNO→（SN，AGE，DEPT，MN），SCD（SNO，SN，AGE，DEPT，MN，CNO，SCORE）=A[SNO，SN，AGE，DEPT，MN]⋈B[SNO，CNO，SCORE]，也就是说，用其投影在SNO上的自然连接可复原关系模式SCD
这一性质非常重要，在后面的关系规范化中要用到。

函数依赖的分类

完全函数依赖与部分函数依赖
- 设关系模式R(U)，U是属性全集，X和Y是U的子集
- 如果，并且对于X的任何一个真子集X′ ，都有 $⇸$ ，则称Y对X完全函数依赖（Full Functional Dependency），记作。
- 如果对X的某个真子集X′ ，有，则称Y对部分函数依赖（Partial Functional Dependency），记作。
  例如，在关系模式SCD中，因为 $⇸$ ，且CNO ⇸ SCORE，所以有：。
  而SNO→AGE，所以
由上述定义可知：
只有当决定因素是组合属性时，讨论部分函数依赖才有意义，当决定因素是单属性时，只能是完全函数依赖。
例如，在关系模式S（SNO，SN，AGE，DEPT），决定因素为单属性SNO，有SNO→（SN，AGE，DEPT），不存在部分函数依赖。
传递函数依赖
- 设有关系模式R（U），U是属性全集，X，Y，Z是U的子集，
- 若，但 $⇸$ ，而，则称Z对X传递函数依赖（Transitive Functional Dependency），记作：。
- 如果，则，这时称Z对X直接函数依赖，而不是传递函数依赖。
  例如，在关系模式SCD中，SNO→DEPTN，但DEPTN ⇸ SNO，而DEPTN→MN，则有。当学生不存在重名的情况下，有SNO→SN，SN→SNO，，SN→DEPTN，这时DEPTN对SNO是直接函数依赖，而不是传递函数依赖。
  综上所述，函数依赖分为完全函数依赖、部分函数依赖和传递函数依赖三类，它们是规范化理论的依据和规范化程度的准则

用函数依赖定义候选键

设为关系模式中的属性或属性组合。若，则K称为R的一个候选键（Candidate Key）。
若关系模式R有多个候选键，则选定其中的一个做为主键（Primarykey）。
若k是R的一个候选键，并且S⊃K，则称S是R的一个超键 (Super Key)
在任一候选键中出现过的属性称为主属性；主属性之外的称为非主属性

!!! 求解关系的候选解

对于关系模式，其中是R中所有属性的集合，是上的一组函数依赖，根据中属性在中出现的特点，分成如下四类：
- L类属性：只在中某个函数依赖的左部出现。
- R类属性：只在中某个函数依赖的右部出现。
- LR类属性：在中某个函数依赖的左部和右部均出现。
- N类属性：在中每个函数依赖左部和右部均不出现。
L类和N类属性必然是候选键中的属性
R类属性必然不是候选键中的属性
LR类属性有可能是候选键中的属性

算法
关系模式𝐑 < 𝐔, 𝐅 >，其中𝐔 = {𝑨𝟏, 𝑨𝟐, … , 𝑨𝒏}是R中所有属性的集合

求解和类属性
根据的特点，划分属性类别（重点检验和类属性）。令为类和类属性集的并集，为类属性集的集合。
若，则(L,N)为唯一候选键。
求解属性集关于上的函数依赖集的闭包。如果包含了的全部属性，则是的唯一候选键，算法结束。否则，转算法步骤3
若，则找类。
遍历中的单一属性，并与构成属性组，如果，则为候选键，令，转算法步骤4。
如果在上一步找到所有的候选键，则算法结束。否则，遍历中的任意两个、三个属性（记为），并与构成属性组，如果，且不包含已有的候选键，则为新计算的候选键。

用函数依赖定义外键

关系模式 R 中属性或属性组 X 并非 R 的候选键，但 X 是另一个关系模式的候选键，则称 X 是R 的外键（Foreign key）

2 范式

规范化的基本思想是消除关系模式中的数据冗余，消除数据依赖中的不合适的部分，解决数据插入、删除时发生的异常现象。
这就要求关系数据库设计出来的关系模式要满足一定的条件。
我们把关系数据库的规范化过程中为不同程度的规范化要求设立的不同标准称为范式（Normal Form）。
由于规范化的程度不同，就产生了不同的范式。
- 满足最基本规范化要求的关系模式叫第一范式，
- 在第一范式中进一步满足一些要求为第二范式，
- 以此类推就产生了第三范式等概念。
每种范式都规定了一些限制约束条件。
一个低一级范式的关系模式，通过模式分解转化为若干个高一级范式的关系模式的集合，这种分解过程叫作关系模式的规范化（Normalization）
各种范式之间存在联系：
某一关系模式R为第n范式，可简记为 R ∈ nNF。

规范化设计

1NF

第一范式（First Normal Form）是最基本的规范形式，即关系中每个属性都是不可再分的简单项。
定义：如果关系模式R，其所有的属性均为简单属性，即每个属性域都是不可再分的，则称R属于第一范式，简称1NF，记作R ∈ 1NF。
如地址是可再分的属性：北京市海淀区花园路街道
第一范式排除了多值属性、组合属性

缺点

一个关系模式仅仅属于第一范式是不够的。在前面给出的关系模式SCD属于第一范式，但其具有大量的数据冗余，具有插入异常、删除异常、更新异常等弊端。
为什么会出现这些问题呢？
分析一下SCD中的函数依赖关系，它的关系键是（SNO，CNO）的属性组合，所以有如下函数依赖：
由此可见，在SCD中，既存在完全函数依赖，又存在部分函数依赖和传递函数依赖。
由于关系中存在着复杂的函数依赖，才导致数据操作中出现了种弊端。
克服这些弊端的方法是用投影运算将关系分解，去掉过于复杂的函数依赖关系，向更高一级的范式进行转换。

2NF

定义
如果关系模式R ∈ 1NF，且每个非主属性都完全函数依赖于R的每个关系键，则称R属于第二范式（Second Normal Form），简称2NF，记作R ∈ 2NF。（去掉非主键的部分依赖）

在关系模式SCD中，SNO，CNO为主属性，AGE，DEPT，MN，MN，SCORE均为非主属性，经前述分析，存在非主属性对关系键的部分函数依赖，所以SCD不是2NF。

将SCD分解成三个关系模式S，D，SC：
学生关系S(SNO,SN,AGE,DEPT)
选课关系SC(SNO,CNO,SCORE)
系关系D(DEPT,MN)

其中S的关系键为SNO，D的关系键为DEPT，都是单属性，不可能存在部分函数依赖。而对于SC，。所以SCD分解后，消除了非主属性对关系键的部分函数依赖，S，D，SC均属于2NF

又如关系模式TCS（T，C，S）

一个教师可以讲授多门课程，一门课程可以是多个教师讲授

同样一个学生可以选听多门课程，一门课程可以为多个学生选听

(T,C,S)三个属性的组合是关系键，T,C,S都是主属性，而无非主属性，所以也就不可能存在非主属性对关系键的部分函数依赖，TCS ∈ 2NF。

性质

从1NF关系中消除非主属性对关系键的部分函数依赖，则可得到2NF关系。
如果R的关系键为单属性，或R的全体属性均为主属性，则R ∈ 2NF。

2NF规范化

2NF规范化是指把1NF关系模式通过投影分解转换成2NF关系模式的集合。
分解时遵循的基本原则就是“一事一表”，让一个关系只描述一个实体或者实体间的联系。如果多于一个实体或联系，则进行投影分解。

2NF规范化的形式化描述
设关系模式R（X，Y，Z），R ∈ 1NF，但R不是2NF，其中，X是主属性，Y，Z是非主属性，且存在部分函数依赖，。设X可表示为X1、X2，其中。则R（X，Y，Z）可以分解为R[X1，Y]和R[X，Z]

因为，所以R(X，Y，Z)=R[X1，Y] ⋈ R[X1，X2，Z]=R[X1，Y] ⋈ R[X，Z]，即R等于其投影R[X1，Y]和[X，Z]在X1上的自然连接，R的分解具有无损连接性。
由于，因此R[X1，Y] ∈ 2NF。若R[X，Z]不属于2NF，可以按照上述方法继续进行投影分解，直到将R[X，Z]分解为属于2NF关系的集合，且这种分解必定是有限的

下面以关系模式SCD为例，来说明2NF规范化的过程

SCD(SNO,SN,AGE,DEPT,MN,CNO,SCORE)

由SNO→SN，SNO→AGE，SNO→DEPT，（SNO，CNO）⎯ ⎯f → SCORE，可以判断，关系SCD至少描述了两个实体：

一个为学生实体，属性有SNO、SN、AGE、DEPT、MN；

另一个是学生与课程的联系（选课），属性有SNO、CNO和SCORE。

根据投影分解的原则，我们可以将SCD分解成两个关系

SD(SNO,SN,AGE,DEPT，MN)，描述学生实体；

SC(SNO,CNO,SCORE)，描述学生与课程的联系。

对于分解后的两个关系SD和SC，主键分别为SNO和（SNO，CNO），非主属性对主键完全函数依赖。因此，SD∈ 2NF，SC ∈ 2NF，而且前面已经讨论，SCD的这种分解没有丢失任何信息，具有无损连接性。

优点

消除了一些数据冗余
部分解决插入异常（把学生的基本信息与选课信息分开存储，则学生基本信息因没选课而不能插入的问题得到了解决）
部分解决删除异常（如果某个学生不再选修C1课程，只在选课关系SC中删去该该学生选修C1的记录即可，而SD中有关该学生的其它信息不会受到任何影响）

缺点

数据冗余。每个系名和系主任的名字存储的次数等于该系的学生人数。
插入异常。当一个新系没有招生时，有关该系的信息无法插入。
删除异常。某系学生全部毕业而没有招生时，删除全部学生的记录也随之删除了该系的有关信息。
更新异常。更换系主任时，仍需改动较多的学生记录。

之所以存在这些问题，是由于在SCD中存在着非主属性对主键的传递依赖
分析SCD中的函数依赖关系，SNO→SN，SNO→AGE，SNO→DEPT，DEPT→MN，SNO MN ⎯⎯t→ ，非主属性MN对主键SNO传递依赖

3NF

定义
如果关系模式R ∈ 2NF，且每个非主属性都不传递依赖于R的每个关系键，则称R属于第三范式（Third Normal Form），简称3NF，记作R ∈ 3NF。（去掉非主键的传递依赖）

性质

如果R ∈ 3NF，则R也是2NF。
如果R ∈ 2NF，则R不一定是3NF。

3NF规范化
把2NF关系模式通过投影分解转换成3NF关系模式的集合。和2NF规范化时遵循的原则相同，即“一事一表”，让一个关系只描述一个实体或者实体间的联系。

例：将SD(SNO,SN,AGE,DEPT,MN)规范到3NF。

分析SD的属性组成，可以判断，关系SD实际上描述了两个实体：

一个为学生实体，属性有SNO，SN，AGE，DEPT；

另一个是系的实体，其属性DEPT和MN。

根据投影分解的原则，我们可以将SD分解成如下两个关系

S(SNO,SN,AGE,DEPT)，描述学生实体；

D(DEPT，MN)，描述系的实体。

对于分解后的两个关系S和D，主键分别为SNO和DEPT，不存在非主属性对主键的传递函数依赖。因此，S ∈ 3NF，D ∈ 3NF。

优点

数据冗余降低。
不存在插入异常。
不存在删除异常。
不存在更新异常。

缺点

3NF只限制了非主属性对键的依赖关系，而没有限制主属性对键的依赖关系。
如果发生了这种依赖，仍有可能存在数据冗余、插入异常、删除异常和修改异常

考虑关系模式SNC（SNO，SN，CNO，SCORE），其中SNO代表学号，SN代表学生姓名并假设没有重名，CNO代表课程号，SCORE代表成绩。可以判定，SNC有两个候选键（SNO，CNO）和（SN，CNO），其函数依赖如下：

唯一的非主属性SCORE对键不存在部分函数依赖，也不存在传递函数依赖。所以SNC∈3NF。

因为，即决定因素SNO或SN不包含候选键，从另一个角度说，存在着主属性对键的部分函数依赖：，
由于存在着这种主属性对键的部分函数依赖关系，造成了关系SNC中存在着较大的数据冗余，学生姓名的存储次数等于该生所选的课程数，从而会引起修改异常。
若学生没有选课，则无法记录学生的姓名信息，或学号信息，产生插入异常。
若学生所有课程都退选了，则会删除学生的学号姓名信息对照信息，产生删除异常。

BCNF

定义
如果关系模式R ∈ 1NF，且所有的函数依赖X→Y（Y ∉ X），决定因素X都包含了R的一个候选键，则称R属于BC范式（Boyce-Codd Normal Form），记作R ∈ BCNF。（去掉主键的部分依赖和传递依赖）

BCNF性质

满足BCNF的关系将消除任何属性（主属性或非主属性）对键的部分函数依赖和传递函数依赖。也就是说，如果R ∈ BCNF，则R也是3NF。
如果R ∈ 3NF，则R不一定是BCNF

BCNF规范化：BCNF规范化是指把3NF关系模式通过投影分解转换成BCNF关系模式的集合。

例将SNC(SNO,SN,CNO，SCORE)规范到BCNF。
分析SNC数据冗余的原因，是因为在这一个关系中存在两个实体，一个为学生实体，属性有SNO、SN；另一个是选课实体，属性有SNO、CNO和SCORE
根据投影分解的原则，我们可以将SNC分解成如下两个关系：

S1(SNO,SN)，描述学生实体；

S2(SNO,CNO,SCORE)，描述学生与课程的联系。
对于S1，有两个候选键SNO和SN，
对于S2，主键为（SNO，CNO）。
在这两个关系中，无论主属性还是非主属性都不存在对键的部分依赖和传递依赖，S1 ∈ BCNF，S2 ∈ BCNF。

如果一个关系数据库中所有关系模式都属于3NF，则已在很大程度上消除了插入异常和删除异常，但由于可能存在主属性对候选键的部分依赖和传递依赖，因此关系模式的分离仍不够彻底。
如果一个关系数据库中所有关系模式都属于BCNF，那么在函数依赖的范畴内，已经实现了模式的彻底分解，消除了产生插入异常和删除异常的根源，而且数据冗余也减少到极小程度

关系模式规范化

目的
是使结构合理，消除存储异常，使数据冗余尽量小，便于插入、删除和更新。

步骤
规范化就是对原关系进行投影，消除决定属性不是候选键的任何函数依赖。具体可以分为以下几步：

对1NF关系进行投影，消除原关系中非主属性对键的部分函数依赖，将1NF关系转换成若干个2NF关系。
对2NF关系进行投影，消除原关系中非主属性对键的传递函数依赖，将2NF关系转换成若干个3NF关系。
对3NF关系进行投影，消除原关系中主属性对键的部分函数依赖和传递函数依赖，也就是说使决定因素都包含一个候选键。得到一组BCNF关系。

在实际应用中，最有价值的是3NF和BCNF，在进行关系模式的设计时，通常分解到3NF就足够了

非规范化设计

许多数据库应用场景强调性能优先
规范化设计有时会导致数据库运行效率的下降
非规范化设计
在特殊条件和要求下，适当地降低甚至抛弃关系模式的范式，不再要求一个表只描述一个实体或者实体间的一种联系。其主要目的在于提高数据库的运行效率
一般认为，在下列情况下可以考虑进行非规范化处理：
- 大量频繁的查询过程所涉及的表都需要进行连接；
- 主要的应用程序在执行时要将表连接起来进行查询；
- 对数据的计算需要临时表或进行复杂的查询。
非规范化处理的主要技术包括增加冗余或派生列，对表进行合并、分割或增加重复表等。
无论使用何种非规范化技术，都需要一定的管理来维护数据的完整性
管理方式较常采用的是用触发器来实现。对数据的任何修改立即触发对复制列或派生列的相应修改。触发器是实时的，而且相应的处理逻辑只在一个地方出现，易于维护

增加冗余列

增加冗余列是指在多个表中具有相同的列，它常用来在查询时避免连接操作，但它需要更多的存储空间，同时增加表维护的工作量。

例如，如果经常检索一门课的任课教师姓名，则需要做class和teacher表的连接查询：
select classname,teachername from class,teacher where class.teacherNo=teacher.teacherNo
这样的话就可以在class表中增加一列 teacher_name，就不需要连接操作了。

增加派生列

增加派生列指增加的列来自其它表中的数据，由它们计算生成。它的作用是在查询时减少连接操作，避免使用集函数。派生列除于冗余列同样的缺点之外，还需消耗计算资源在数据变化时对派生列的值进行及时维护。

重新组表

重新组表指如果许多用户需要查看两个表连接出来的结果数据，则把这两个表重新组成一个表来减少连接而提高性能，但需要更多的磁盘空间，同时也损失了数据在概念上的独立性

例如，用户经常需要同时查看课程号，课程名称，任课教师号，任课教师姓名，则可把表class(classno,classname,teacherno) 和表teacher(teacherno,teachername) 合并成一个表class_Teacher(classno,classname,teacherno,teachername)。

表分割

对表做分割可以提高性能，特别是在进行大数据量管理时，常采用“分库分表”策略
表分割有两种方式：

水平分割
垂直分割

水平分割

根据一列或多列数据的值把数据行放到两个独立的表中。
分割方法包括范围分区、散列分区、列表分区等
水平分割通常在下面的情况下使用：
- 表很大，分割后可以降低在查询时需要读的数据和索引的页数，同时也降低了索引的层数，提高查询速度。
- 表中的数据本来就有独立性，例如表中分别记录各个地区的数据或不同时期的数据，特别是有些数据常用，而另外一些数据不常用。
需要把数据存放到多个介质上。

垂直分割

把主键和一些列放到一个表，然后把主键和另外的列放到另一个表中。
如果一个表中某些列常用，而另外一些列不常用，就可以采用垂直分割加快查询速度。其缺点是需要管理冗余列，查询所有数据需要join操作。

特点

非规范化设计的主要优点
- 减少了查询操作所需的连接
- 减少了外部键和索引的数量
- 可以预先进行统计计算，提高了查询时的响应速度
非规范化存在的主要问题
- 增加了数据冗余
- 影响数据库的完整性
- 降低了数据更新的速度
- 增加了存储表所占用的物理空间

3 模式分解

关系模式的规范化过程是通过对关系模式的投影分解来实现的，但是投影分解方法不是唯一的，不同的投影分解会得到不同的结果。只有能够保证分解后的关系模式与原关系模式等价的方法才是有意义的。
有哪些分解方法？不同的模式分解方法，为何会产生不同的分解效果？该怎样正确的进行模式分解？该怎样分解到3NF或BCNF？是本节要回答的问题

模式的分解

定义：关系模式的一个分解： $，，，$ ，，且不存在，则称为在上的投影
函数依赖集合的一个覆盖叫作在属性上的投影

数据依赖的公理系统

逻辑蕴含
对于满足一组函数依赖的关系模式 $，$ ，其任何一个关系，若函数依赖都成立, 则称逻辑蕴含
Armstrong公理系统
- 一套推理规则，是模式分解算法的理论基础
- 用途
  - 从一组函数依赖求得蕴含的函数依赖
  - 求给定关系模式的候选键

对关系模式R <U，F >，有以下的推理规则：

A1自反律（Reflexivity）：若，则为所蕴含。
A2增广律（Augmentation）：若为所蕴含，且，则为所蕴含。
A3传递律（Transitivity）：若及为所蕴含，则为所蕴含。
注意：由自反律所得到的函数依赖均是平凡的函数依赖
根据A1，A2，A3这三条推理规则可以得到下面三条推理规则：
- 合并规则：由，有。
- 伪传递规则：由，有。
- 分解规则：由及，有。
根据合并规则和分解规则，可得引理：成立的充分必要条件是成立

函数依赖闭包

在关系模式中为所逻辑蕴含的函数依赖的全体叫作的闭包，记为。
蕴含==导出
定义
设为属性集上的一组函数依赖，，则 $能由根据公理导出$
称为属性集关于函数依赖集的闭包
引理
设为属性集上的一组函数依赖，，能由根据Armstrong公理导出的充分必要条件是
用途
将判定是否能由根据Armstrong公理导出的问题，转化为求出，判定是否为的子集的问题

求属性集X（）关于U上的函数依赖集F 的闭包的算法

输入：X，F
输出：
步骤：
1. 令X(0)=X，i=0
2. 求B，这里；
4. 判断吗
  1. 若相等或 , 则就是, 算法终止。
  2. 若否，则，返回第（2）步。

例
Pasted image 20250523110754.png
Pasted image 20250523110809.png

Pasted image 20250523110940.png

建立公理系统体系目的：从已知的 f 推导出未知的f
有效性：由F出发根据Armstrong公理推导出来的每一个函数依赖一定在F+中
Armstrong公理系统是正确的
完备性：F+中的每一个函数依赖，必定可以由F出发根据Armstrong公理推导出来
Armstrong公理是完备的
所有不能用Armstrong公理推导出来f, 都不为真；若 f 不能用Armstrong公理推导出来， f∉ F+

函数依赖集等价

如果G+=F+，就说函数依赖集 F覆盖G（F是G的覆盖，或G是F的覆盖），或F与G等价。
F+ = G+ 的充分必要条件是
，和
要判定，只须逐一对 F 中的函数依赖X→Y，考察 Y是否属于就行了。

最小依赖集

每一个函数依赖集F 均等价于一个极小函数依赖集Fm。此Fm称为F 的最小依赖集
如果函数依赖集 F 满足下列条件，则称 F 为一个极小函数依赖集。亦称为最小依赖集或最小覆盖。
- F中任一函数依赖的右部仅含有一个属性。
- F中不存在这样的函数依赖X→A，使得F 与 F-{X→A}等价。
- F中不存在这样的函数依赖X→A， X有真子集Z 使得F-{X→A}∪{Z→A}与F等价。

最小依赖集构造方法

依据定义分三步对F 进行“极小化处理”，找出F的一个最小依赖集。

逐一检查中各函数依赖：，若，，则用来取代。
逐一检查中各函数依赖：，令，若，则从中去掉此函数依赖。
逐一取出中各函数依赖：，设，逐一考查，若，则以取代。

模式分解是否正确的判定依据

分解具有无损连接性：R与ρ在数据内容方面是否等价
分解保持函数依赖：R与ρ在函数依赖方面是否等价

无损连接性

关系模式的一个分解 $，$

若与、、…、自然连接的结果相等，则称关系模式的这个分解具有无损连接性（Lossless join）
具有无损连接性的分解保证不丢失信息
无损连接性不一定能解决插入异常、删除异常、修改复杂、数据冗余等问题

无损连接性分解的判定方法

列表法
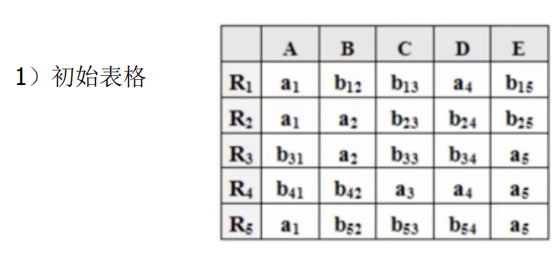
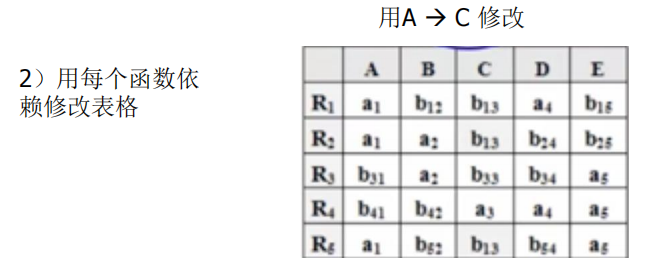
1. 构造一个k行n列的二维表T，第i 行对应于一个关系模式Ri，第j列对应于属性Aj，令：tij=aj，若Aj属于Ri；否则tij=bij。
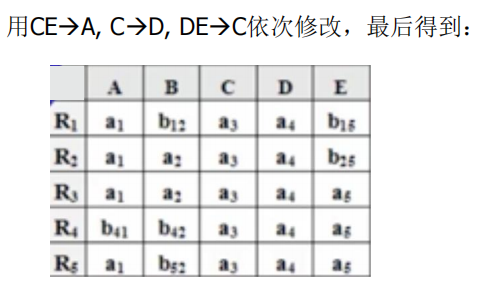
2. 对于F中一个FD：X→Y，如果表格中有两行在X分量上相等，在Y分量上不相等，那么把这两行在Y分量上改成相等。如果Y的分量中有一个是aj，那么另一个也改成aj；如果没有aj，那么用其中的一个bij替换另一个(尽量把ij改成较小的数，亦即取i 值较小的那个)
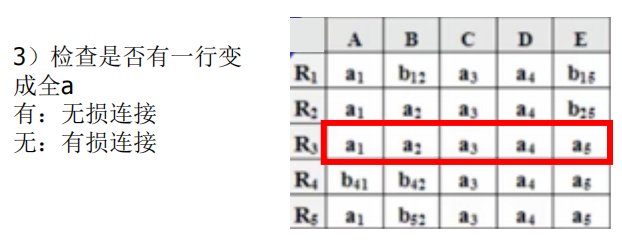
3. 若在修改的过程中，发现表格中有一行全是a，即a1 ,a2 ,…,an，那么可立即断定ρ 相对于F 是无损连接分解，此时不必再继续修改。若经过多次修改直到表格不能修改之后，发现表格中不存在有一行全是a的情况，那么分解就是有损的。特别要注意，这里有个循环反复修改的过程，因为一次修改可能导致表格能继续修改。
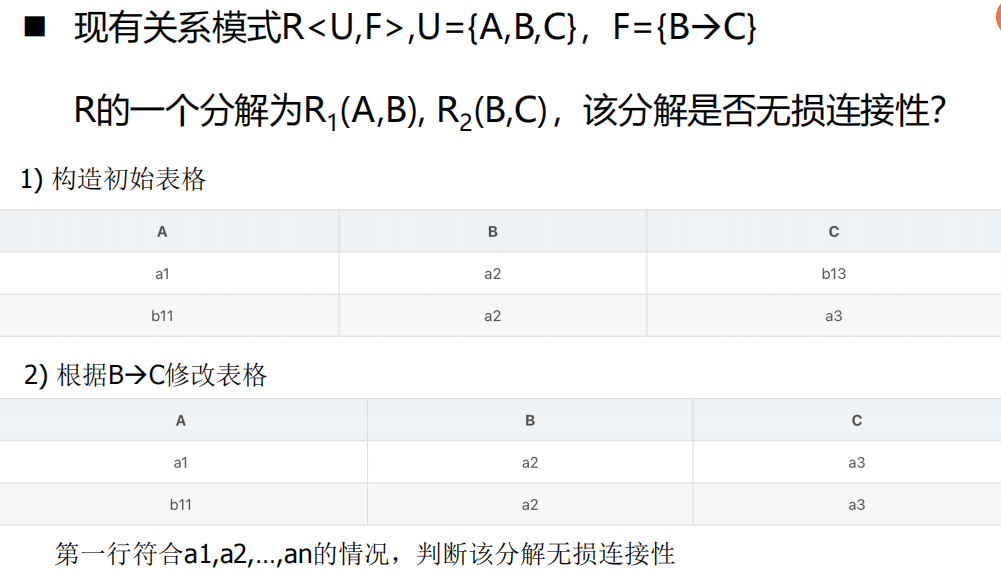
定理法(适合关系模式R分解为两个关系模式R1、R2时)
- 定理：若关系模式中，被分解为是R的一个分解，若或者，则称具有无损连接性
- 示例：已知 $，$ ，R的一个分解为
  解：为，为, 因为，因此分解是无损连接
- 设关系模式R 具有函数依赖集F， $，，，$ 是R的一个分解，且是关于F无损连接性的分解，则有：对特定i，设, 是Ri关于Fi的无损连接分解，则R到 $，$ 的分解是关于F 无损连接的。

函数依赖保持性

设关系模式 $，$ 被分解为若干个关系模式，其中，且不存在，Fi为F在Ui上的投影。如果F 所蕴含的任意一个函数依赖一定也由所蕴含，则称关系模式R的分解具有函数依赖保持性。

函数依赖保持性的判定方法

Pasted image 20250523145038.png
Pasted image 20250523145047.png
Pasted image 20250523145144.png
Pasted image 20250523145154.png
Pasted image 20250523145128.png

无损连接性与函数依赖保持性

分解具有无损连接性和分解保持函数依赖是两个互相独立的标准。具有无损连接性的分解不一定能够保持函数依赖。同样，保持函数依赖的分解也不一定具有无损连接性。
Pasted image 20250523114312.png

（了解）怎样正确的分解到3NF和BCNF

分解到BCNF的无损链接分解法
分解到3NF的保持依赖分解法
分解到3NF的既保持依赖，又无损连接的分解法