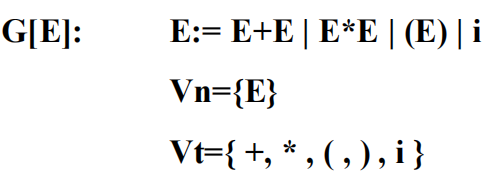2.1 预备知识-形式语言基础
1 字母表和符号串
- 字母表:符号的非空有限集 例:
- 符号:字母表中的元素 例:
- 符号串:符号的有穷序列 例:
形式定义:
有字母表- 若x是
- y是
- 空符号串:无任何符号的符号串 (
- 符号串集合:由符号串构成的集合。
2 符号串和符号串集合的运算
- 符号串相等:x=y iff组成x的每一个符号和组成y的每一个符号依次相等。
- 符号串的长度:x为符号串,其长度
例: x=STV , |x|=3。 - 符号串的联接:若x、y是定义在Σ上的符号串,且x=XY,y=YX,则 x 和 y 的联接 xy=XYYX也是Σ上的符号串。
注意:一般xy≠yx,而εx=xε - 符号串集合的乘积运算:令A、B为符号串集合,定义
A={a,b}, B={c,d}, AB={ac,ad,bc,bd}
因为εx=xε=x,所以{ε}A = A{ε} = A - 符号串集合的幂运算:有符号串集合A,定义
= - 符号串集合的闭包运算:设A是符号串集合,定义
= =
例:A={x,y}
=
2.2 文法的非形式讨论
- 文法:文法是对语言结构的定义与描述。即从形式上用于描述和规定语言结构的称为“文法”(或称为“语法”),不涉及语义。
例:有一句子:“我是大学生” 。这是一个在语法、语义上都正确的句子,该句子的结构(称为语法结构)是由它的语法决定的 。在本例中它为“主谓结构”。 - 语法规则 ::= ->:我们通过建立一组规则,来描述句子的语法结构。
<句子>::=<主语><谓语>
<主语>::=<代词>|<名词>
<代词> ::=你|我|他
<名词>::= 王民|大学生|工人|英语
<谓语>::=<动词><直接宾语>
<动词>::=是|学习
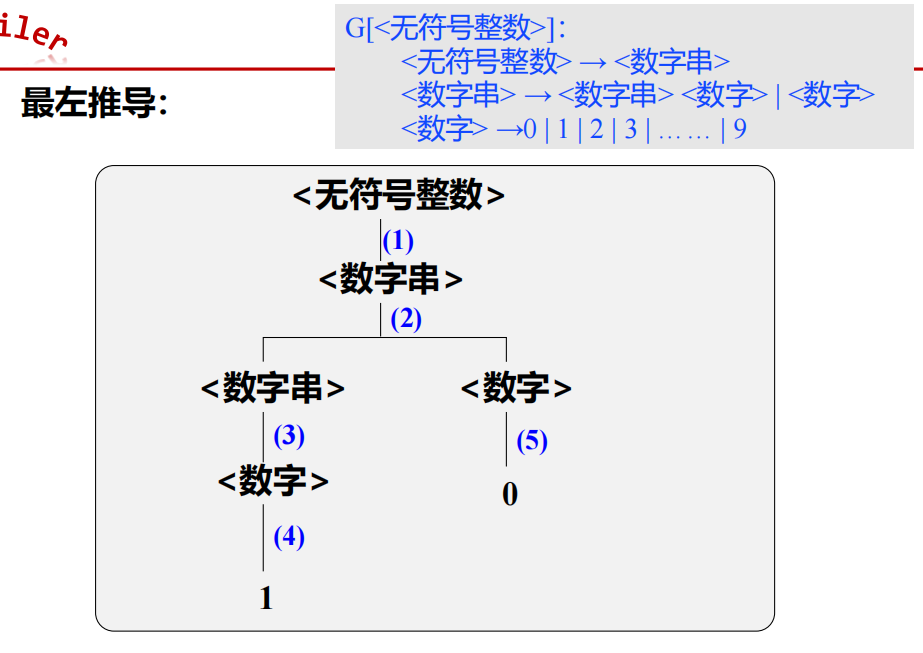
<直接宾语>::=<代词>|<名词> - 由规则推导 => 句子:有了一组规则之后,可以按照一定的方式用它们去推导或产生句子。
推导方法:从一个要识别的符号开始推导,即用相应规则的右部来替代规则的左部,每次仅用一条规则去进行推导。- 多步推导:
- 最左推导:从最左的语法成分进行推导
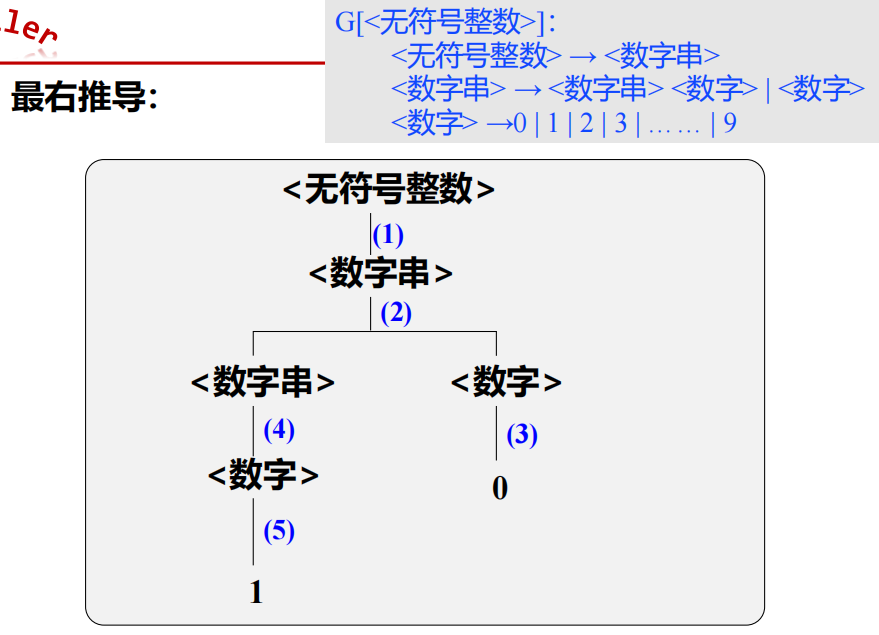
- 最右推导(规范推导/一般推导)
- 多步推导:
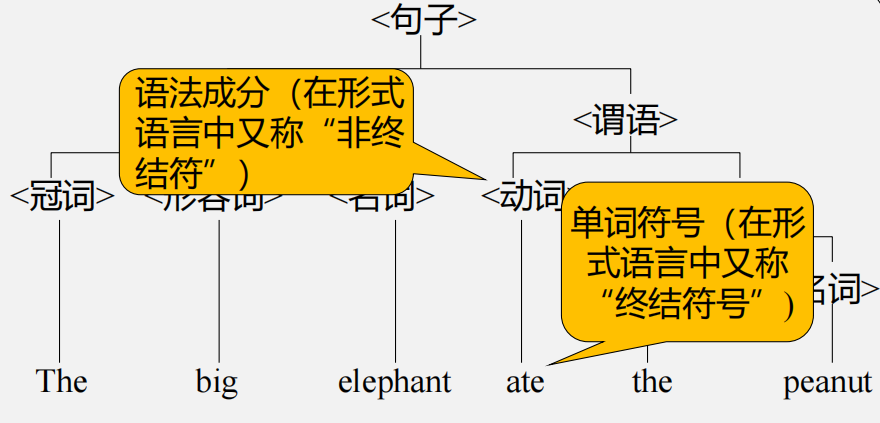
- 语法树们:用来描述一个句子的语法结构。
- 非终结符/中间结点
- 终结符号/叶子结点
2.3 文法和语言的形式定义
2.3.1 文法的定义
- 文法
规则:是一个有序对
- 有的产生式具有相同的左部,可以合在一起。
- 给定一个文法,实际只需给出产生式集合,并指定识别符号。(识别符号一般约定为第一条规则的左部符号)
2.3.2 推导的形式定义
- 直接推导
文法= , = 其 中
若 , 则
若 = = , 有 , 则
- 间接推导
文 法 ,
则
文 法 或 则 - 规范推导(最右推导):有
2.3.3 语言的形式定义
- 文法
- 句型:x是句型,iff
且
推导时的它本身/中间步骤/终结符号 - 句子:x是句子,iff
且
推导至少一步见到的东西,是一堆终结符号 - 语言:
句子的集合
- 句型:x是句型,iff
形式语言理论可以证明以下两点
- 等价文法:G和G’是两个不同的文法,若 L(G) = L(G’) ,则G和G’为等价文法。
2.3.4 递归文法
- 递归规则:规则右部有与左部相同的符号
- 对于
- 若
- 若
- 对于
- 递归文法:文法G,存在U ∈Vn
- if
- if
- if
- if
- 左递归文法的缺点:不能用自顶向下的方法来进行语法分析
- 递归文法的优点:可用有穷条规则,定义无穷语言
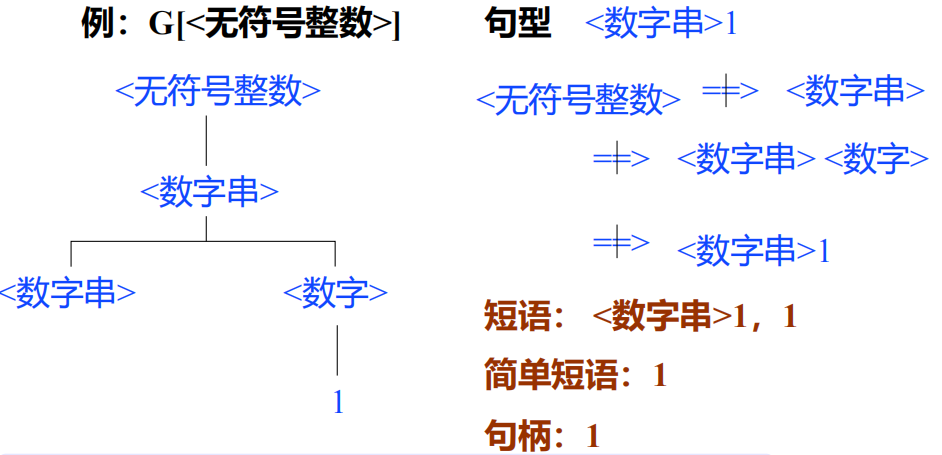
2.3.5 句型的短语、简单短语和句柄
- 给定文法
- 若
- 若
其中, ,
- 若
- 直观理解:短语是前面句型中的某个非终结符所能推出的符号串。
- 任何句型本身一定是相对于识别符号Z的短语。
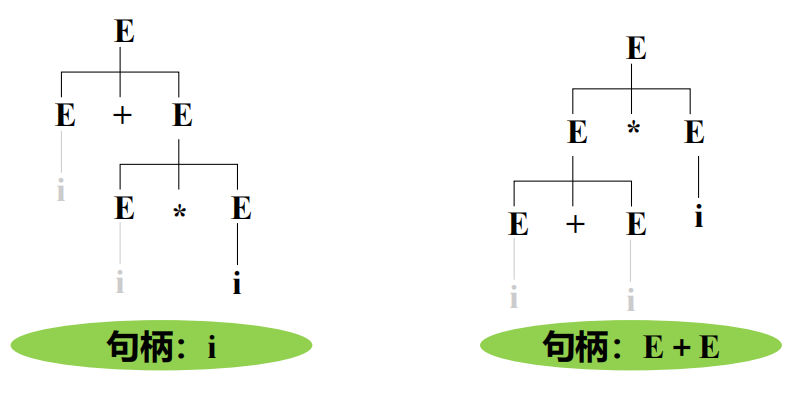
- 任一句型的最左简单短语称为该句型的句柄。
- 短语、简单短语是相对于句型而言。一个句型可能有多个短语、简单短语,但句柄只能有一个。
给定句型找句柄的步骤:
短语 -> 简单短语 -> 句柄
- 短语、简单短语是相对于句型而言。一个句型可能有多个短语、简单短语,但句柄只能有一个。
例题
2.4 语法树与二义性
2.4.1 推导与语法树
-
语法树:句子结构的图示表示法,它是一种有向图,由结点和有向边组成。
- 结点:符号
- 根结点:识别符号
- 中间结点:非终结符
- 叶结点:终结符或非终结符
- 有向边:表示结点间的派生关系。
- 结点:符号
-
句型的推导及语法树的生成(自顶向下)
给定G[Z],句型w:
可建立推导序列,
可建立语法树,以Z为树根结点,每步推导生成语法树的一枝,最终可生成句型的语法树。
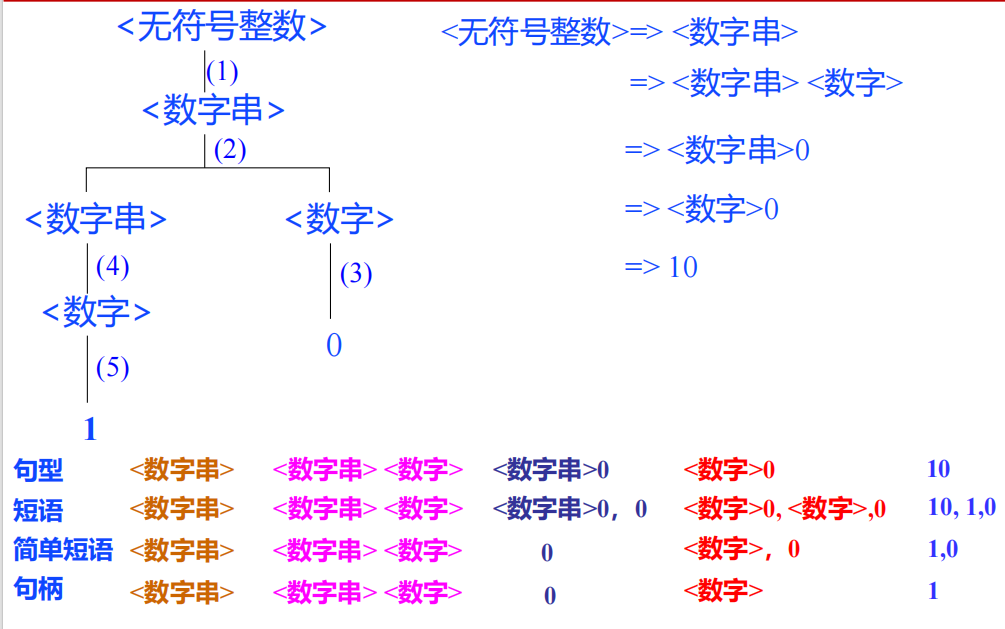
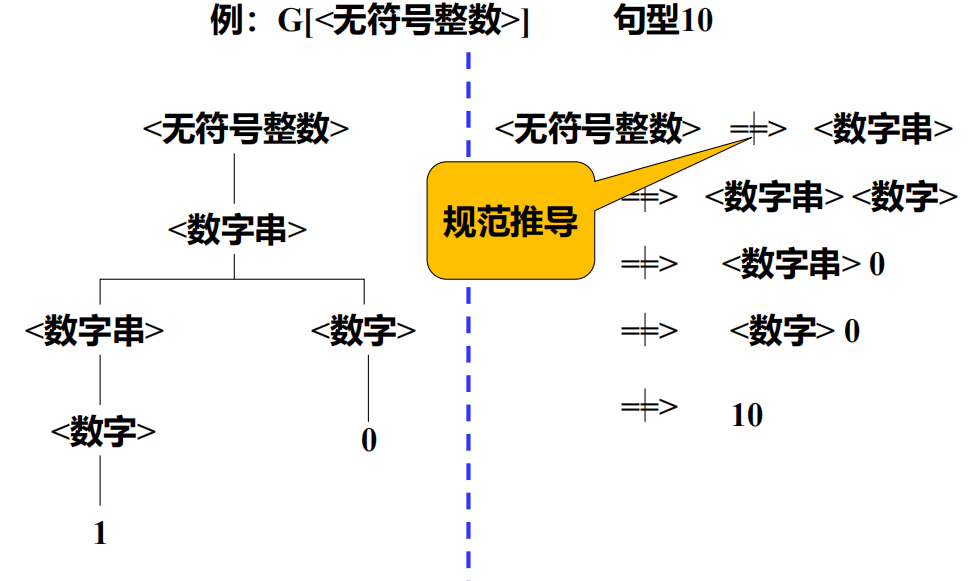
1, 0, 10是短语,都能由前面的V_n 推出来
1, 0是简单短语,能由 <数字> 通过一步推出来,而10不可以
1是句柄,是最左简单短语 -
子树与短语
- 子树:语法树中的某个结点(子树的根)连同它向下派生的部分所组成。
- 某子树的末端结点按自左向右顺序为句型中的符号串,则该符号串为该句型的相对于该子树根的短语。
- 只需画出句型的语法树,然后根据子树找短语→简单短语→句柄。
-
树与推导
句型推导过程<==>句型语法树的生长过程- 由推导构造语法树
从识别符号开始,自右向左建立推导序列
=>
由根结点开始,自上而下建立语法树
- 由语法树构造推导
自下而上地修剪子树的末端结点,直至把整棵树剪掉(留根),每剪一次对应一次规约。
=>
从句型开始,自左向右地逐步进行规约,建立推导序列。
12. 对句型中最左简单短语(句柄)进行的规约称为规范规约。
通常我们每次都剪掉当前句型的句柄(最左简单短语),即每次均进行规范归约
- 由推导构造语法树
-
通过规范推导或规范规约所得到的句型称为规范句型。
2.4.2 文法的二义性
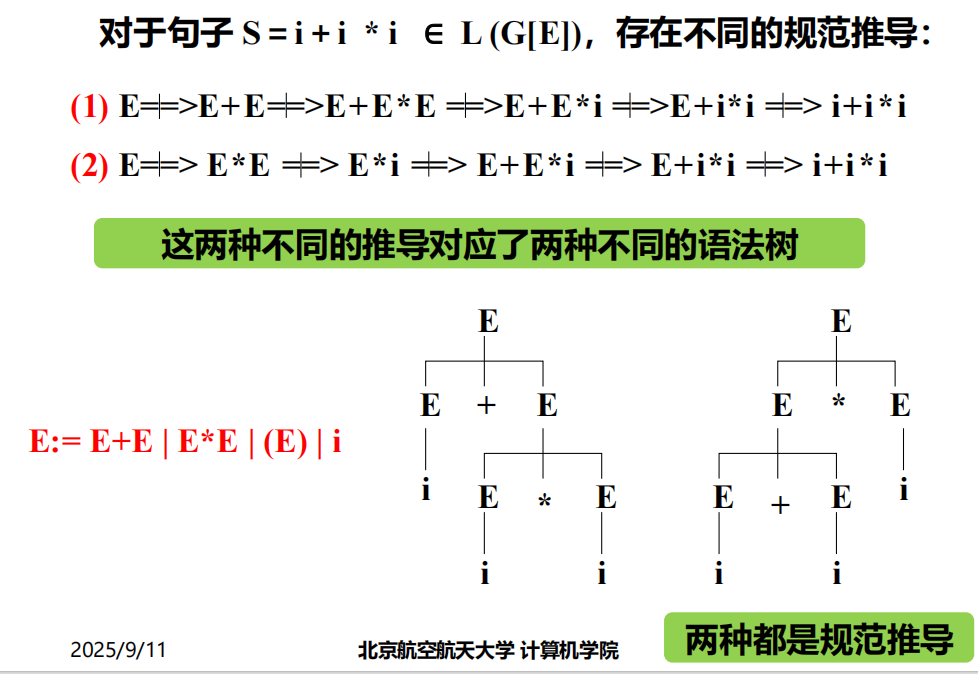
- 若对于一个文法的某一句子存在两棵不同的语法树,则该文法是二义性文法,否则是无二义性文法。
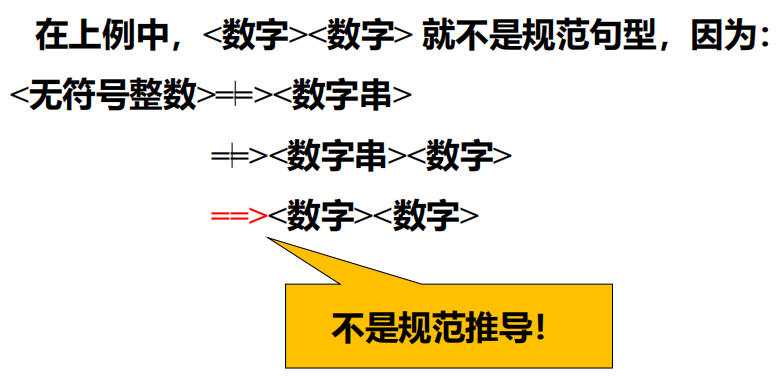
- 若一个文法的某句子存在两个不同的规范推导,则该文法是二义性的,否则是无二义性的。
- 若一个文法的某规范句型的句柄不唯一,则该文法是二义性的,否则是无二义性的。
对于句型
若文法是二义性的,则在编译时就会产生不确定性。
遗憾的是在理论上已经证明:文法的二义性是不可判定的,即不可能构造出一个算法,通过有限步骤来判定任一文法是否有二义性。
法1:提出一些限制条件,称为无二义性的充分条件。当文法满足这些条件时,就可以判定文法是无二义性的
法2:即不改变二义性文法,而是确定一种编译算法,使该算法满足无二义性充分条件。
2.5 有关文法的实用限制
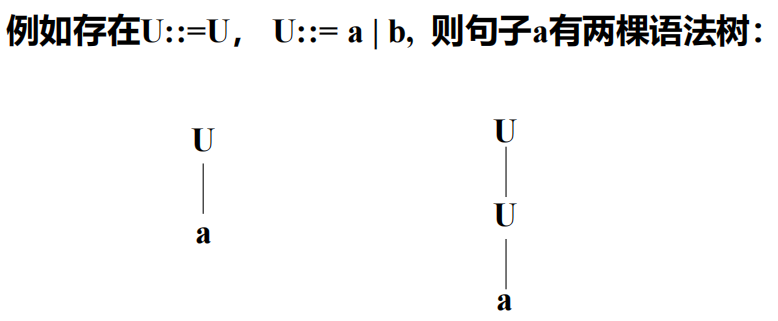
- 有害规则:若文法中有如U::=U的规则,则这就是有害规则,它会引起二义性。
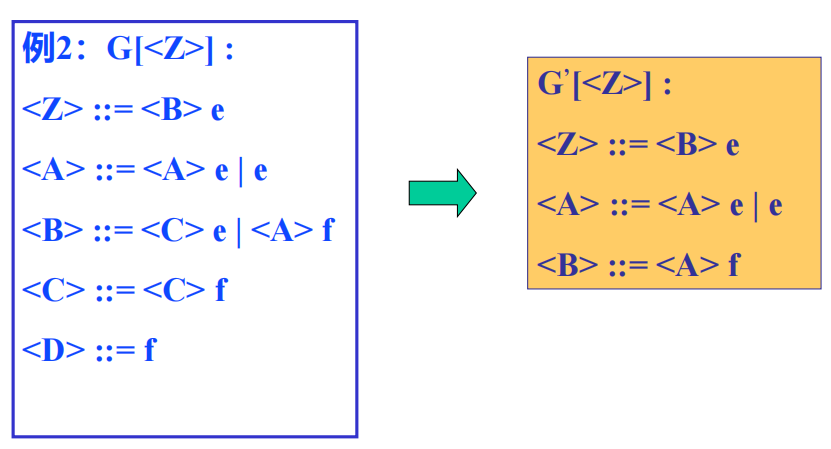
- 多余规则
- 在推导文法的所有句子中,始终用不到的规则。即该规则的左部非终结符不出现在任何句型中。
- 在推导句子的过程中,一旦使用了该规则,将推不出任何终结符号串。即该规则中含有推不出任何终结符号串的非终结符。
- 若某文法中无有害规则或多余规则,则称该文法是压缩过的。
例
2.6 文法的其它表示法
例:
- 扩充的BNF表示(Backus Normal Form)
- BNF的元符号: <, >, ::=, |
- 扩充的BNF的元符号: <, >, ::=, |, {, }, [, ], (, )
() 表示把符号组合起来
{} 表示重复0-n次
[] 表示出现0-1次
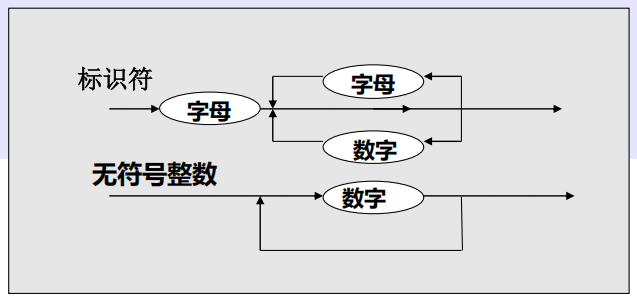
- 语法图
2.7 文法和语言分类
- 形式语言:用文法和自动机所描述的没有语义的语言。
- 文法定义:四元组:G= ( Vn,Vt,P,Z )
- 语言定义:
文法和语言分类:
0型
其 中 - 0型文法称为短语结构文法。规则的左部和右部都可以是符号串,一个短语可以产生另一个短语。
- 0型语言:L0,这种语言可以用图灵机(Turing)接受。
1型
: 其 中 - 称为上下文敏感或上下文有关。也即只有在x、y这样的上下文中才能把U改写为u。
- 1型语言:L1,这种语言可以由一种线性界限自动机接受。
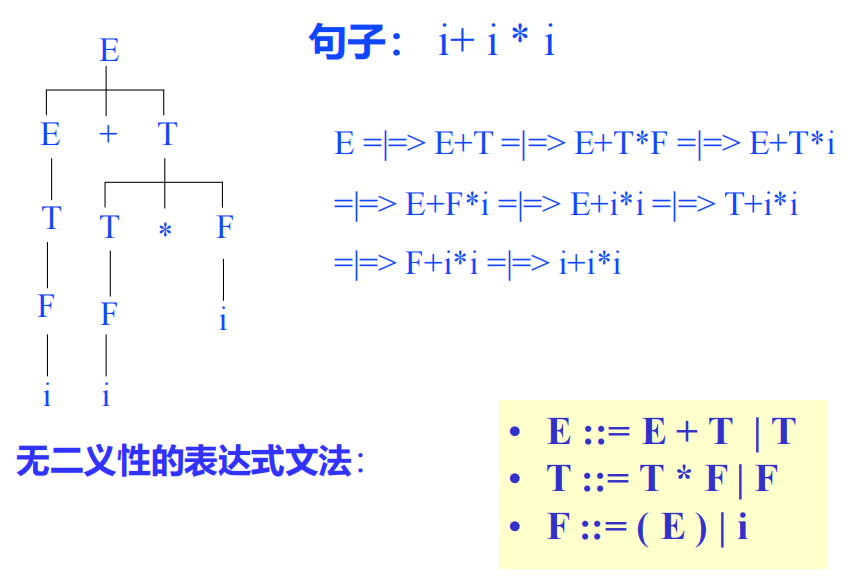
2型!
其 中 - 称为上下文无关文法。也即把 U 改写为 u 时,不必考虑上下文。
- 1型文法的规则中x,y均为 ε 时即为2型文法
- 注意:2型文法与BNF表示相等价。
- 2型语言:L2 这种语言可以由下推自动机接受。
3型!
- 左线性:
或 其 中 - 右线性:
或 其 中 - 3型文法称为正则文法。它是对2型文法进行进一步限制
- 3型语言:L3,又称正则语言、正则集合,这种语言可以由有穷自动机接受。
根据上述讨论,
0型文法可以产生L0、L1、L2、L3,
2 型文法只能产生L2、L3,不能产生L0、L1
3型文法只能产生L3,词法分析中用的比较多